Numpy初了解（如何创建Ndarray数组+numpy数据类型+切片+广播）

Python科学计算基础——Numpy

基本介绍略去，直接记录学习笔记。运行工具为jupyter notebook。

#安装jupyter notebook
pip install notebook
# help
jupyter notebook --help
# 配置文件目录查看
jupyter notebook --generate-config
# 修改文件存放路径 jupyter_notebook_config.py
c.NotebookApp.notebook_dir = 'D:\jupyter'

创建Ndarray数组。

# 一维数组，利用序列对象创建
a = np.array([1,2,3])
a
>array([1, 2, 3])
# 二维
b = np.array([[1,2,3],[4,5,6]])
b
>array([[1, 2, 3],
       [4, 5, 6]])
#判断维数
b.ndim
#判断形状，2行3列
b.shape
>(2, 3)
# numpy自带的快速填充方法
np.ones((2,3)) # np.ones(shape, dtype=None, order='C')
>array([[1., 1., 1.],
       [1., 1., 1.]])
# 三维数组
np.zeros((2,3,4))
# 快速初始化ndarray的第三种方法
# empty初始化出来的变量并非固定
np.empty((2,3,2))
# 第四种方法，类似列表的range函数
np.arange(5,15,2)
>array([ 5,  7,  9, 11, 13])

# 改变ndarray形状
# 后面的数组形状理应和前面的序列数量相同
np.arange(16).reshape((2,2,4))
>array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7]],

       [[ 8,  9, 10, 11],
        [12, 13, 14, 15]]])
# 如果不知道序列数量呢？
# 不指定，则num默认为50
# np.linspace? 均匀分布
np.linspace(1,10,num=4)
>array([ 1.,  4.,  7., 10.])

Numpy数据类型。

主要使用的有以下几种，选择不同的类型对计算的速度会有影响，例如float64精度肯定比float16会慢一些

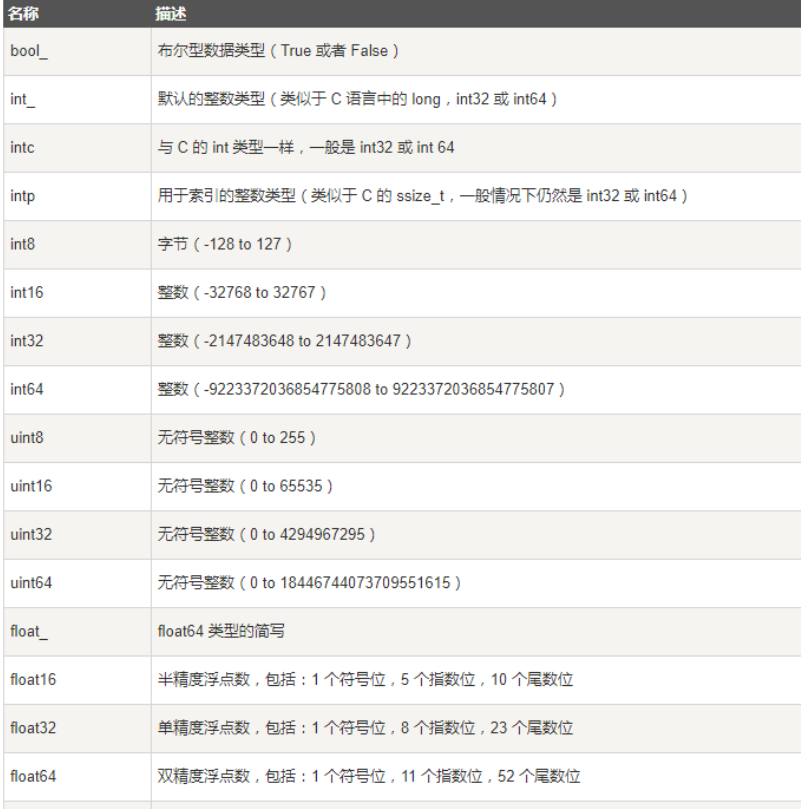
如果不指定数据类型，则numpy自动推测数据类型

a = np.array([1,2,3])
a.dtype
>dtype('int32')

a = np.array([True,True,False])
a.dtype
>dtype('bool')

直接指定数据类型也可以

a = np.array([1,2,3],dtype="float16")
a.dtype
>dtype('float16')

我们可以使用astype改变原始数据的类型

a = np.array([True,True,False])
a.astype("int32")
>array([1, 1, 0])

但是当我们使用astype修改浮点类型的数据时，有一些事项需要注意，下方示例中转化整形之后，小数点之后的数字都被去除

a = np.array([1.2,2.56,3.69])
a.astype('int32')
>array([1, 2, 3])

这和numpy的round函数有点相似，文档如下

a.round(decimals=0, out=None)
Return `a` with each element rounded to the given number of decimals.

测试代码如下，rounded本意就是四舍五入：

a = np.array([1.2,2.56,3.69])
a.round(0)
>array([1., 3., 4.])
a.round(1)
>array([1.2, 2.6, 3.7])

数据的切片和索引

类似于python中的切片，numpy切片出来的数据其实是源数据的一个引用（或者叫做“视图”），而非拷贝（不是新数组！），这句话如何理解，测试代码如下：

a = np.arange(10)
a
>array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

a[1:3]
>array([1, 2])

a[1:3] = 666
a
>array([  0, 666, 666,   3,   4,   5,   6,   7,   8,   9])

我们可以看到当我对numpy数组中的切片进行修改，原始array数据也发生了变化，这是出于节省机器内存的考虑，由于numpy经常用于处理大量的数据，如果频繁拷贝会占据额外的机器内存，因此当我们对切片进行修改时会自动广播到原始array中。

我们也可以使用步长来切片

a[1::2]
>array([666,   3,   5,   7,   9])

a[::-1]
>array([  9,   8,   7,   6,   5,   4,   3, 666, 666,   0])

a[-5:]
>array([5, 6, 7, 8, 9])

高维数组的切片

#高维数组
a = np.arange(24).reshape(2,3,4)
a
>array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
        
a[0]
>array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
# 取某一个数值
a[0][0][3]
>3
# 缩写如下，等同于上方代码
a[0,0,3]

# 花式切片，例如取第一维后两行数据
a[0,1:]
>array([[ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

# 取第一维后两行数据前两列数据
a[0,1:,:2]
>array([[4, 5],
       [8, 9]]

关于高维数组中的bool取值，例如取值大于12，我们可以将bool值当作索引来进行取值

(a>10)&(a<20)
>array([[[False, False, False, False],
        [False, False, False, False],
        [False, False, False,  True]],

       [[ True,  True,  True,  True],
        [ True,  True,  True,  True],
        [False, False, False, False]]])

a[(a>10)&(a<20)]
>array([11, 12, 13, 14, 15, 16, 17, 18, 19])

Numpy的广播与数组操作

当我想要对numpy数组里面的每个值进行加减乘除，由于广播的特性，这是很容易解决的。

a = np.arange(12).reshape(2,6)
a
>array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11]])
#相加
a + 10
>array([[10, 11, 12, 13, 14, 15],
       [16, 17, 18, 19, 20, 21]])
# 如果两个形状相同的array，则会自动对位处理
a+a
>array([[ 0,  2,  4,  6,  8, 10],
       [12, 14, 16, 18, 20, 22]])
# 如果列数相同，维度不同，则自动将每一行与新数组作处理
b = np.arange(6)
b
>array([0, 1, 2, 3, 4, 5])

a + b
> array([[ 0,  2,  4,  6,  8, 10],
       [ 6,  8, 10, 12, 14, 16]])

关于矩阵乘法，搞了很久才搞懂

a
>array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11]])

# 转置,即对换数组的维度。The transposed array.
a.T
> array([[ 0,  6],
       [ 1,  7],
       [ 2,  8],
       [ 3,  9],
       [ 4, 10],
       [ 5, 11]])
# 等用于上方的转置，但更为强大，可对高维数组转置
a.transpose()  
# 矩阵乘法
np.dot(a,a.T)
>array([[ 55, 145],
       [145, 451]])

矩阵乘法的定义为矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和，例如，

# 矩阵A为
[[1,2],
  [3,4]]
# 矩阵B为
[[5,6],
[7,8]]

矩阵乘法结果为

[[19,22],
[43,50]]

第1行第1列的值19位1*5+2*7，第1行第2列的值22为1*6+2*8，第2行第1列的值43为3*5+4*7，第2行第2列的值50为3*6+4*8。

看完这个小例子，我们再来看上面的第一个array值为55就知道怎么算出来的：

0*0+1*1+2*2+3*3+4*4+5*5=55

如何将所有高维数据扁平化呢？即返回一维数组。

#返回一个迭代器
a.flat
><numpy.flatiter at 0x229f9303bc0>
for i in a.flat:
    print(i)

for i in a.flat:
    print(i)
=>
0
1
2
3
4
5
6
7
8
9
10
11

#第二种方法是返回一维数组的副本
a.flatten()
>array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

b = a.flatten()
b[1] =777
b
>array([  0, 777,   2,   3,   4,   5,   6,   7,   8,   9,  10,  11])
a
>array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11]])


# 第三种方法返回原始数据的一维数组视图
b=a.ravel()
b
>array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
b[2]=666
a
>array([[  0,   1, 666,   3,   4,   5],
       [  6,   7,   8,   9,  10,  11]])

参阅：

#jupyter notebook
https://jupyter.org/install
https://www.jianshu.com/p/91365f343585
# 转置
https://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html

YOLO813

Numpy初了解（如何创建Ndarray数组+numpy数据类型+切片+广播）