分类问题中最简单的是二分类，但其实多分类也可以分解成一个个二分类来解决。Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。本质上来说，逻辑回归和线性回归都属于广义线性模型，但他们两个要解决的问题不一样，逻辑回归解决的是分类问题，输出的是离散值，线性回归解决的是回归问题，输出的连续值

    在逻辑回归中，最常用的是Sigmoid函数，Sigmoid函数的数学形式是：

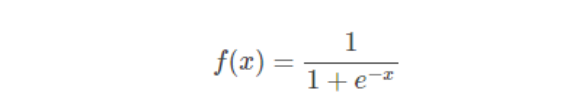
    函数图像为

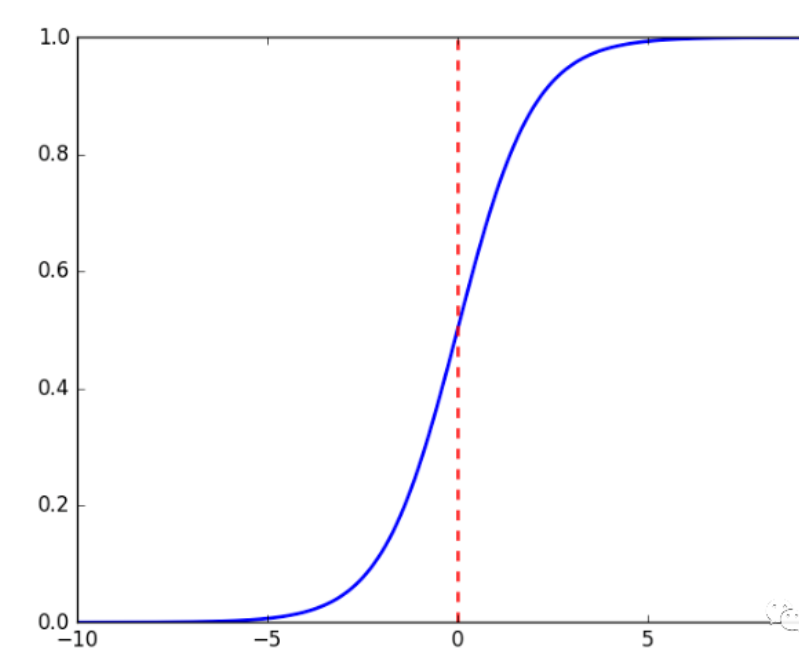
    sigmoid函数以(0,0.5)中心对称，当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。

    Sigmoid函数的值域范围限制在(0,1)之间，我们知道[0,1]与概率值的范围是相对应的，这样sigmoid函数就能与一个概率分布联系起来了。

    之前在多元线性回归文章中，写了一个方程式

y=a*x1+b*x2+c*x3+d

    在线性回归中，上面方程式输出的y值为因变量，但是逻辑回归通过函数L将a*x1+b*x2+c*x3+d对应一个隐状态p，p=L(a*x1+b*x2+c*x3+d),然后根据p 与1-p的大小决定因变量的值。在上面的Sigmoid函数中，应该是将这个y值丢入到公式里面当作x自变量

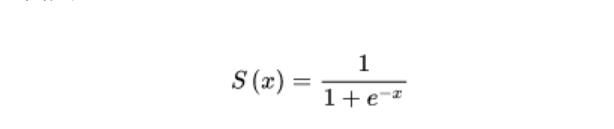
    这其实是一个监督学习的过程，从这个公式来看假设我们已知S(x)，x1， x2，x3，通过算法，我们获取了斜率abc和截距d的值，那么在分类下一批数据时，我们就可以利用这些已知的斜率和截距得出新的数据分类概率。

逻辑回归分类实练

    德国信用卡欺诈数据集，数据来源于互联网。

data.head()

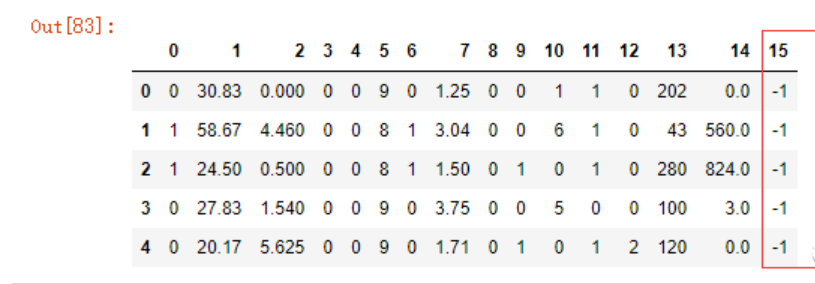
    15项特征，第16项为结果。

data[15].unique()
>array([-1,  1], dtype=int64)

data_x = data[data.columns[:-1]]
data_y = data[15]
data_y

    建立测试数据，前面说过了，逻辑回归其实是一种监督学习，所以我们可以使用train_test_split建立训练和测试数据。

x_train,x_test,y_train,y_test = train_test_split(data_x, data_y)
#逻辑回归
from sklearn.linear_model import LogisticRegression
#ConvergenceWarning: lbfgs failed to converge (status=1)
#请加上max_iter参数
model = LogisticRegression(max_iter=10000)

    和之前的线性回归方法一样训练、预测

model.fit(x_train, y_train)
model.predict(x_test)

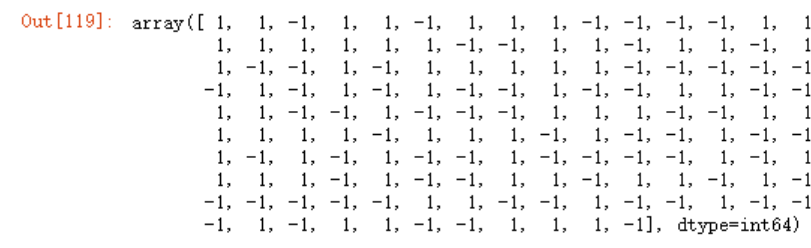
    如果我们想要知道每个分类预测的准确率为多少，可以使用predict_proba函数

model.predict_proba(x_test)

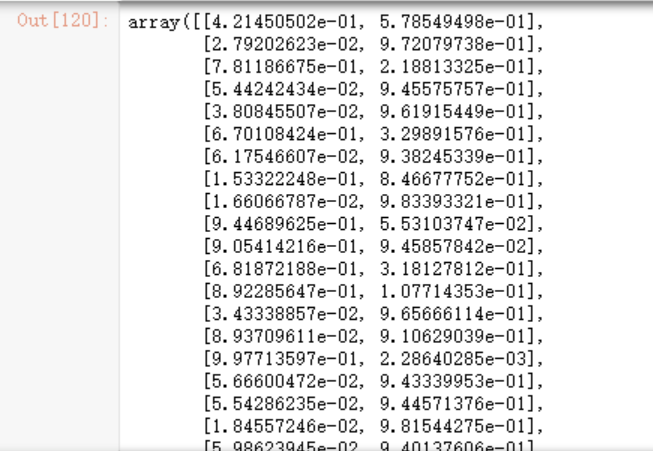
    我们还是按照常规方法来计算准确率

new_df = pd.DataFrame({'orgin':y_test,
                      'pre':model.predict(x_test)})
new_df

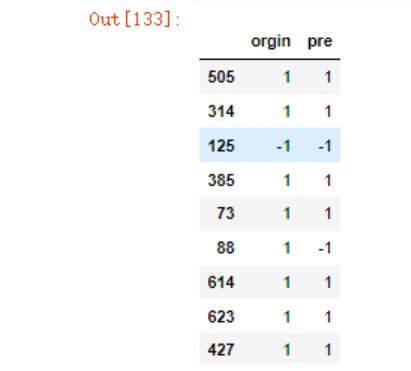
new_df['right'] = new_df.orgin == new_df.pre
new_df

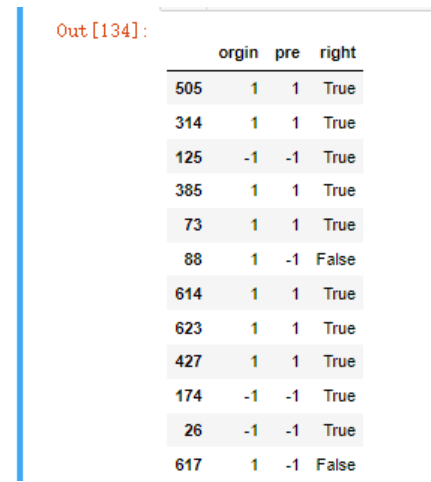
new_df.right.sum()
new_df.right.sum()/len(new_df)

 

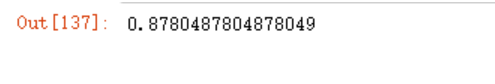
    但其实，我们也可以使用sklearn封装好的accuracy_score函数来计算，例如

from sklearn.metrics import accuracy_score
accuracy_score(model.predict(x_test), y_test)

    可以看到，二者计算的结果是一样的。

 

参考

https://baike.baidu.com/item/Sigmoid%E5%87%BD%E6%95%B0/7981407?fr=aladdin
https://blog.csdn.net/saltriver/article/details/57531963
https://zhuanlan.zhihu.com/p/74874291