机器学习（1）一元线性回归

百度百科中对线性回归的定义：利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为y = w'x+e，e为误差服从均值为0的正态分布。

回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

关于因变量和自变量，因变量（dependent variable）函数中的专业名词，也叫函数值。函数关系式中，某些特定的数会随另一个（或另几个）会变动的数的变动而变动，就称为因变量。如：Y=f(X)。此式表示为：Y随X的变化而变化。Y是因变量，X是自变量。

示例：

x = np.linspace(0,30,20)
x

y = x + np.random.randn(20)
y

plt.figure(figsize=(10,8))
plt.scatter(x,y)

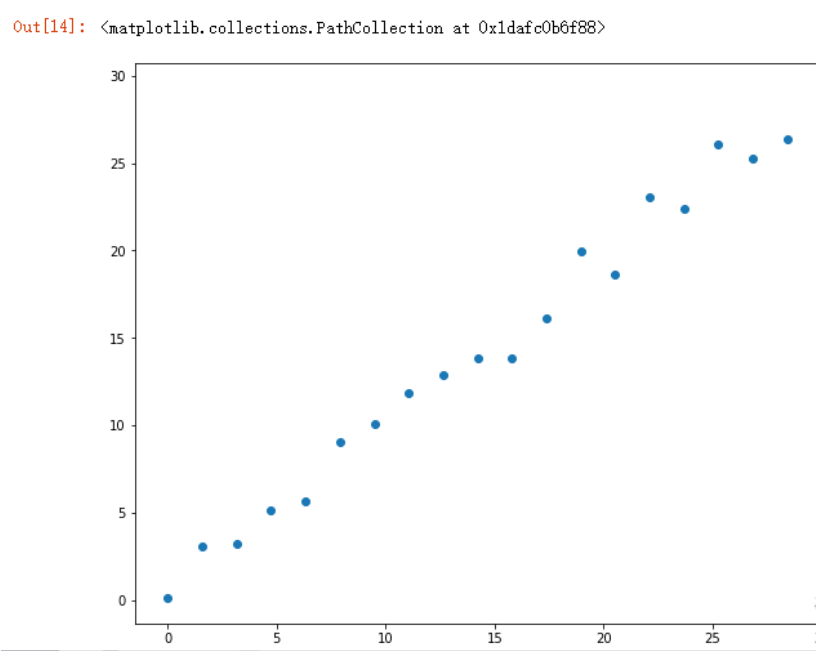
如何预测30以后的数据走势？

首先可以看到这是一个线性的趋势，可以考虑使用线性回归来解决，scikit learn可以很方便的实现线性回归。

#导入线性回归类
from sklearn.linear_model import LinearRegression

#初始化类
model = LinearRegression()
x.shape
>(20,)
x.reshape(-1,1)

x.reshape(-1,1).shape
>(20, 1)

之前在文章中简单了解了下reshape，但是没有用过这种写法，reshape会返回一个新形状的源数据，newshape-整数或整数数组，如(2,3)表示2行3列。新的形状应该与原来的形状兼容，即行数和列数相乘后等于a中元素的数量。如果是整数，则结果将是长度的一维数组，所以这个整数必须等于a中元素数量。若这里是一个整数数组，那么其中一个数据可以为-1。在这种情况下，这个个值python会自动根据第二个数值和剩余维度推断出来。

也就是说上面的x.reshape(-1,1)这种写法与x.reshape(20,1)这种写法是同样的作用，只不过更为简洁、通用，不需要自己输入行数。

test_x = x.reshape(-1,1)
test_y = y.reshape(-1,1)

将数据预处理好之后，就可以丢到初始化的LinearRegression对象中进行fit训练了

model.fit(test_x,test_y)
>LinearRegression()

使用predict函数预测，但是需要注意传递的参数要包裹在中括号里面，

model.predict([[40]])

我们可以尝试把这条线绘制出来，看的更为清晰

plt.scatter(x, y,label='origin')
plt.plot(test_x,
         model.predict(test_x),
         c='r',
        label='predict')
plt.legend()

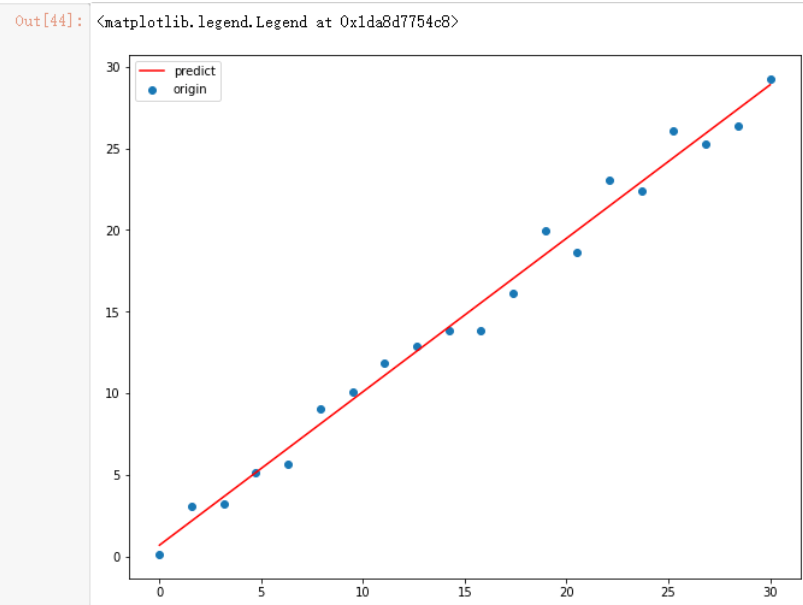
现在我们可以生成一些不在原始数据范围内的测试数据了

x1 = np.linspace(0,45,30).reshape(-1,1)
x1

plt.figure(figsize=(10,8))
plt.scatter(x, y,label='origin')
plt.plot(x1,
         model.predict(x1),
         c='g',
        label='predict')
plt.legend()

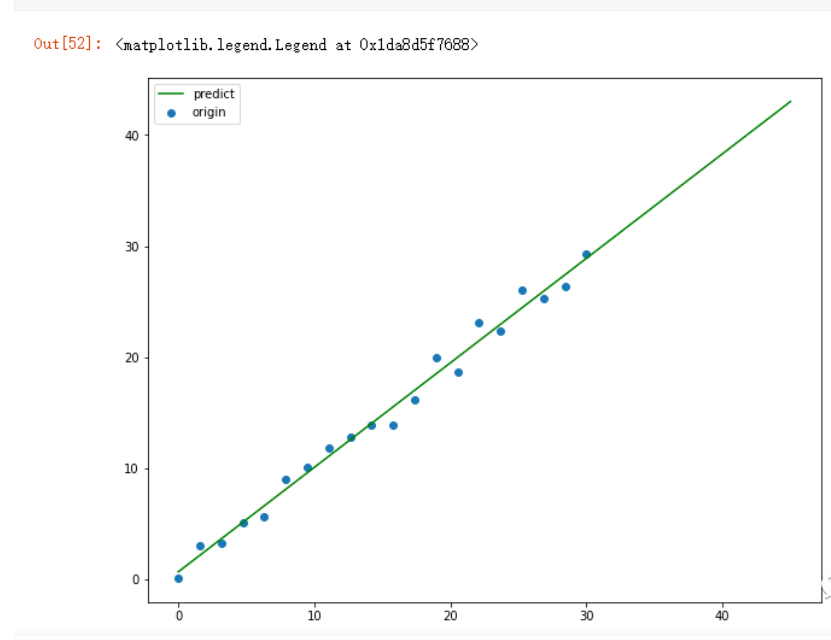
那么，我们如何评估这个算法的准确性呢？对于线性函数来说，肯定是所有原始数据点到该线之间的距离之和最小，就是最精准。

但是，这里面有个问题可以考虑一下，我们一定要求点到线的垂直距离吗？我们可以看下点到直线的求值公式

这种方法未免麻烦了点，其实我们想要知道相关性系数，可以采用相同x坐标上，实际点的y坐标减去直线的y坐标来计算，只要后续都按照这个标准来计算，那么相关系数的大小比较绝对是没问题的。

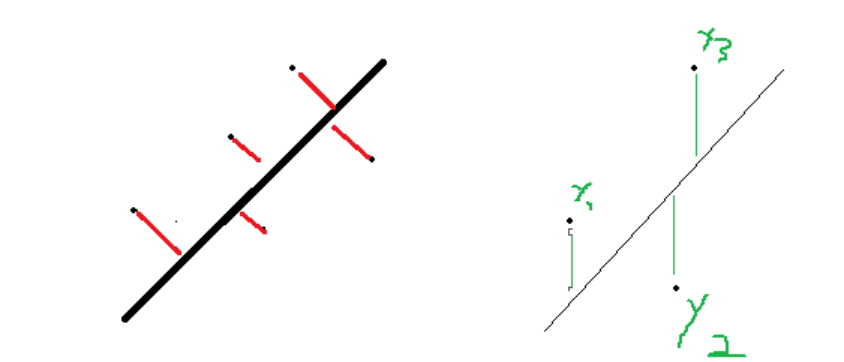
上图中，我们可以采取右侧的这种距离计算方式，照样能算出距离的长短，但是这里会存在一个问题，就是y3减去y是正值，但y2-y就会变成负值，这时候相加没有意义，所以我们还可以利用一个小技巧，因为我们只需要获取相关系数，所以可以使用square函数为每个运算值进行平方再相加。

#原始值y
test_y

# 预测值y
y_predict = model.predict(test_x)
y_predict

np.sum(np.square(test_y - y_predict))
>18.90089821766194

我们可以修改这条直线的斜率，观察之后的距离值，在这之前，我查了下LinearRegression类还有两个属性coef_（模型的斜率）和intercept_（模型的截距，即与y轴的交点），以下图片为一位大佬写的文章截图

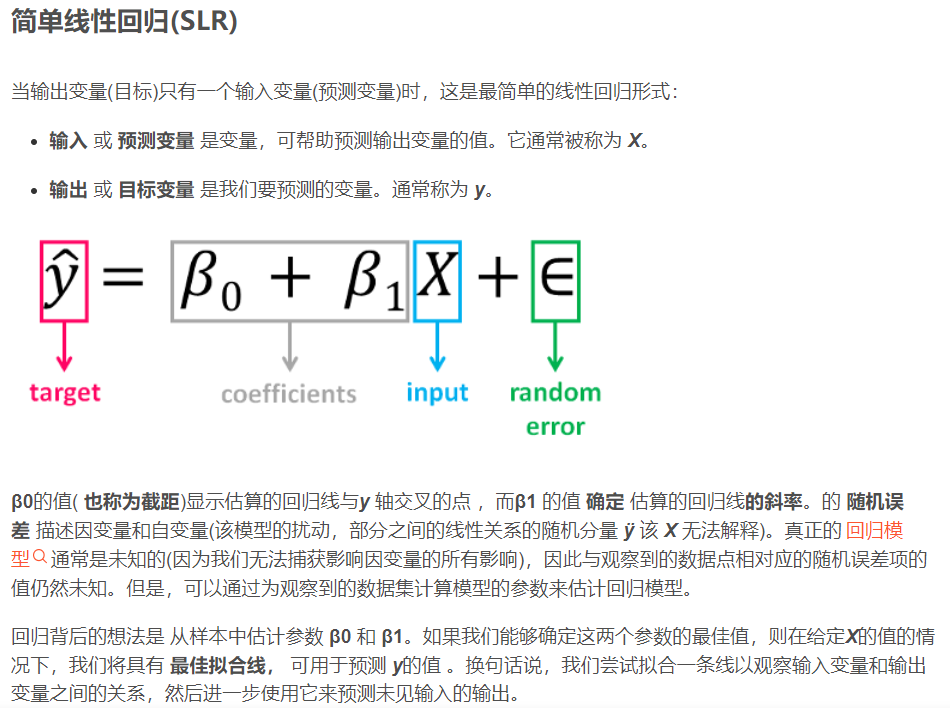
model.intercept_
>array([0.68883066])
model.coef_
>array([[0.94024858]])

现在让我们根据上面这张图片中的β0（截距）和β1（斜率）重新创造一条直线：

#制作一个新的预测值2
y_predict_2 = model.intercept_ + (model.coef_ + 0.5)*test_x
y_predict_2

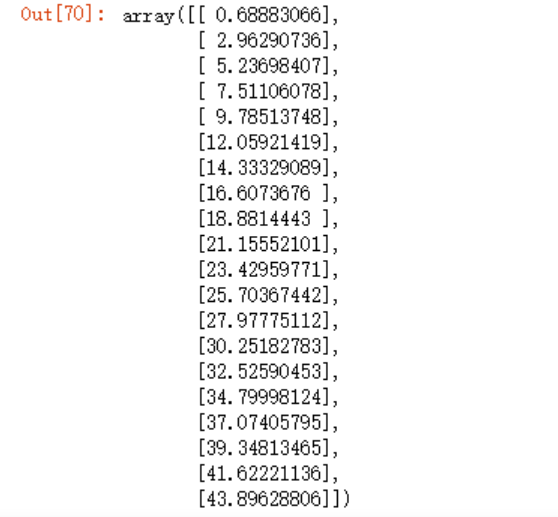
此时，可以看下我们的预测值平方的距离之和远比之前的18.90...大的多

np.sum(np.square(y_predict_2 - test_y ))
>1558.3745824281882

这种预测，不排除前面的数据预测很完美，但是后续的预测出现问题（过拟合），因为所有的样本数据集都拿来训练了，所以最好的方法是取出70%的数据用于样本预测训练，30%留待测试预测的准确率。

X = x.reshape(-1,1)
X
Y = y.reshape(-1,1)
Y

x_train, x_test = X[:14],X[14:]
x_test

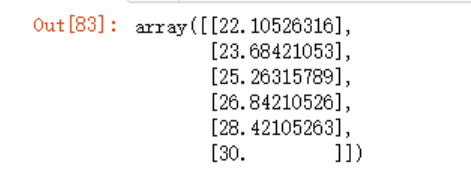
y_train, y_test = Y[:14],Y[14:]
y_test

#训练
model.fit(x_train, y_train)

#预测
y_predict = model.predict(x_test)
y_predict

np.sum(np.square(y_predict - y_test))
>9.54885162285561

#取原来的x_test
#新建一条直线
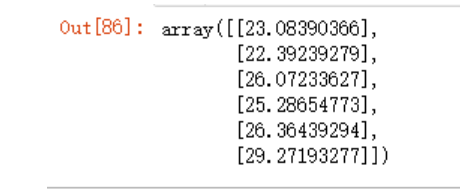
y_predict2 = model.intercept_ + model.coef_*x_test +0.5
y_predict2

np.sum(np.square(y_predict2 - y_test))
>6.8119771944555

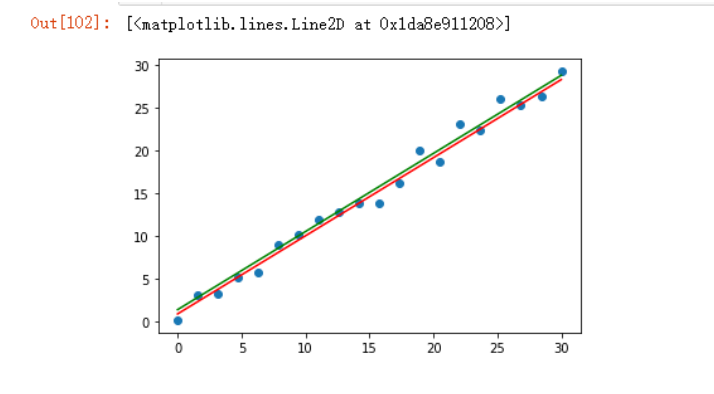
因为是随机数值，系数需要优化很正常，我们可以把这三个图形绘制出来看下，需要注意的是使用plot绘图时，因为选定了X（shape为(20, 1)）坐标，那么预测值Y应该也是同样的shape，而不是x_train（shape：（14,1））或者x_test（shape（6,1））

plt.scatter(X,Y)
plt.plot(X,model.predict(X), color='r')
plt.plot(X, model.intercept_ + model.coef_*X +0.5, color='g')

参考

#截距，斜率
https://blog.csdn.net/weixin_39638014/article/details/111044762

YOLO813

机器学习（1）一元线性回归