机器学习（3）- 聚类KMeans算法初了解

将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他簇中的对象相异。

由于聚类通查不需要使用训练数据学习，在机器学习中也被称为无监督学习。

举个简单的例子，下图中存在很多点的分布，假设我需要将它们分为两类，那么程序会按照所有点到A点、B点的距离来划分成两个类，很明显，C到A的距离比C到B的距离短，所以C会被归为A类，而E到B的距离较短，所以它会被归入B类。

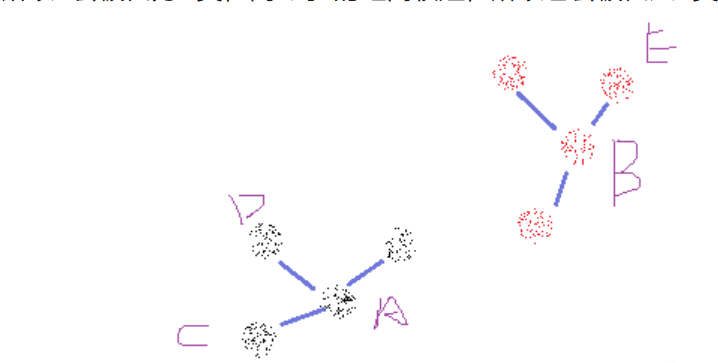
K-Means聚类是以样本间距离为基础，将所有的观测划分到K个群体，使得群体和群体之间的距离尽量大，同时群体内部的观测之间的“距离和”最小。

示例数据：

data1 = pd.DataFrame(
    {'one':np.random.randint(low=1,high=50,size=100),
    'two':np.random.randint(low=50,high=100,size=100)
    })
data1

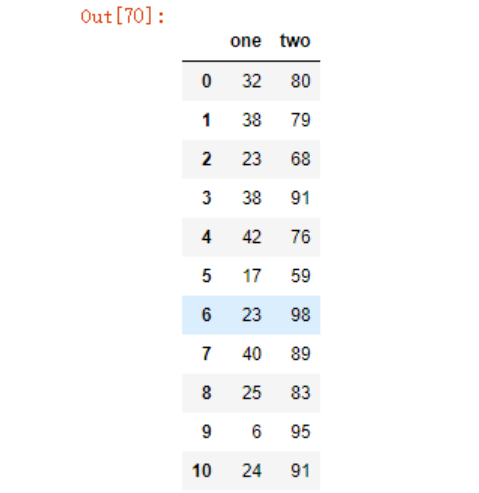
新建测试数据2

data2 = pd.concat([data1, data1+50])
data2

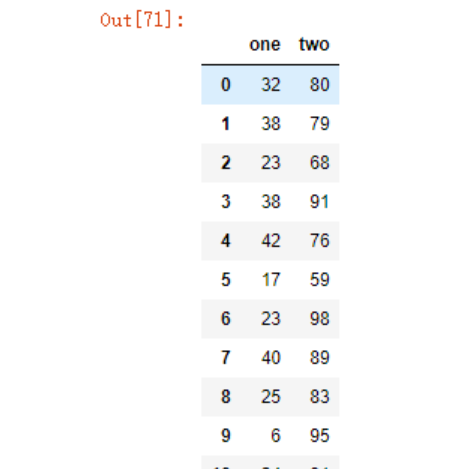
绘制散点图查看分布趋势

plt.style.use('seaborn')
plt.scatter(data2.one, data2.two)

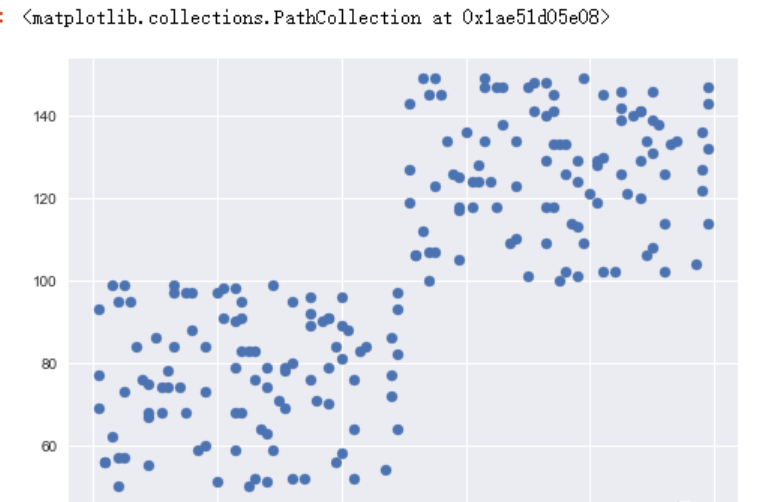
我们现在想要使用K均值聚类的方法将数据分类。

K-means算法原理，先从样本集中随机选取 k 个样本作为簇中心，并计算所有样本与这 k 个“簇中心”的距离，对于每一个样本，将其划分到与其距离最近的“簇中心”所在的簇中，对于新的簇计算各个簇的新的“簇中心”。

选择K个点作为初始质心
repeat
    将每个点指派到最近的质心，形成K个簇
    重新计算每个簇的质心
until 簇不发生变化或达到最大迭代次数

第一步，我们如何确定分成几类？

可以绘图来查看，如上面绘制散点图
从需求出发，例如我们想要区分垃圾邮件
根据聚类指标，多次实验，来看分成几类效果最好

引入Kmeans，cluster本意就有类、簇的含义

from sklearn.cluster import KMeans

先贴官方文档

Init signature:
KMeans(
    n_clusters=8,
    *,
    init='k-means++',
    n_init=10,
    max_iter=300,
    tol=0.0001,
    precompute_distances='deprecated',
    verbose=0,
    random_state=None,
    copy_x=True,
    n_jobs='deprecated',
    algorithm='auto',
)
Docstring:     
K-Means clustering.

上面的数据很明显可以分成两类，我们选择2类来训练预测看看

predict_1 = KMeans(n_clusters=2).fit_predict(data2)
predict_1

可以看到预测的效果还是可以的。

我们再次为散点图加上不同的颜色标记

plt.scatter(data2.one,
            data2.two,
            c=predict_1)

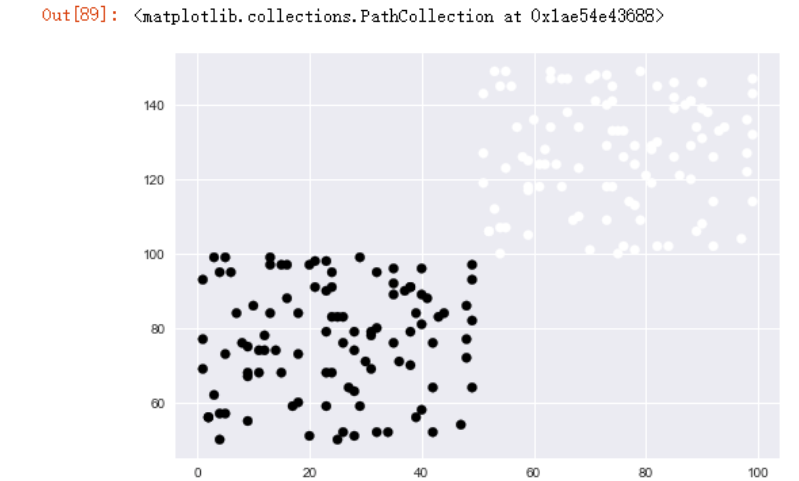
第二步，如何评价聚类的效果？

其实并没有特别可靠的评估方法，同一个类的数据越聚集肯定越好。如果考虑量化来评价的话，以上图论，应该就是左右两个类中的所有点到其中心点的距离最短。

sklearn中的metrics （指标）中有很多评价方法，例如上一篇文章中介绍的mean_squared_error评价线性回归，calinski_harabasz_score函数可以评估聚类，数值越大，则代表聚类越好。

from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(data2,
                        labels=predict_1)

>598.0538963755037

在上面的分类中，我们是通过绘图看到分为两类较为合适，假如说在现在存在一个三维数据，我们就可以calinski_harabasz_score函数逐步实验，获得最优分类，例如我将上面的数据中分为3类

predict_2 = KMeans(n_clusters=3).fit_predict(data2)
predict_2

plt.scatter(data2.one,
            data2.two,
            c=predict_2)

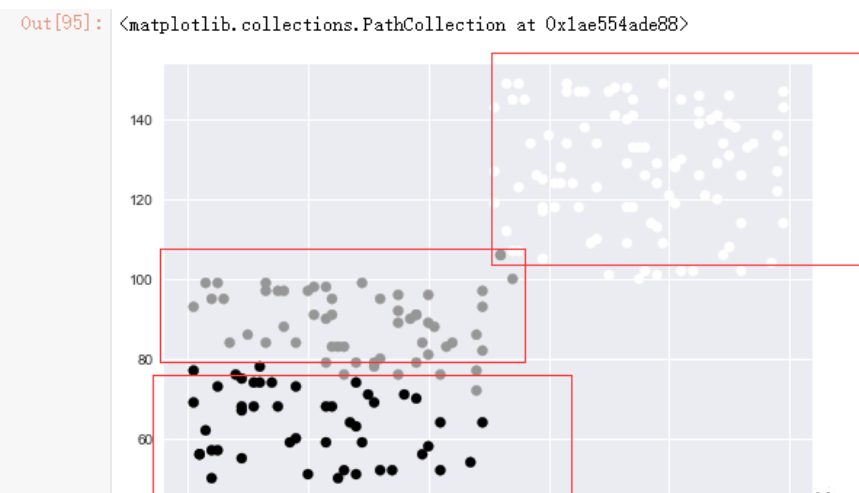
calinski_harabasz_score(data2,
                        labels=predict_2)
>402.39780575634904

可以看到这个值明显要稍微小一点，不如刚刚的聚类效果。

实战测试：小麦数据聚类

数据来源于互联网。

data = pd.read_csv('seeds_dataset.txt',
                  header=None,
                  names=list('abcdefgY'),
                  sep='\s+')
data.head()

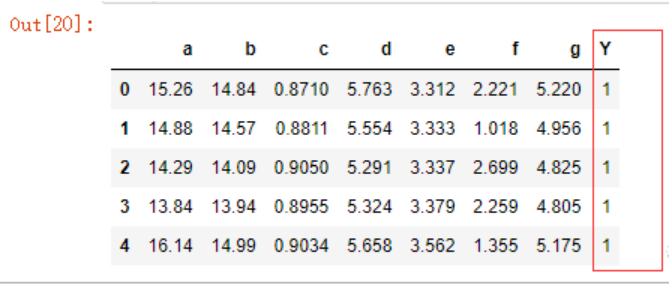
最后一行的Y为种类

data.Y.unique()
>array([1, 2, 3], dtype=int64)

可以看到共有三个类别的小麦。

我们需要通过前面7个类别对数据做成预测，所以只需要选取前7列的数据，关于数据选取，可参考之前的文章

data_x = data.loc[:,'a':'g']
data_x

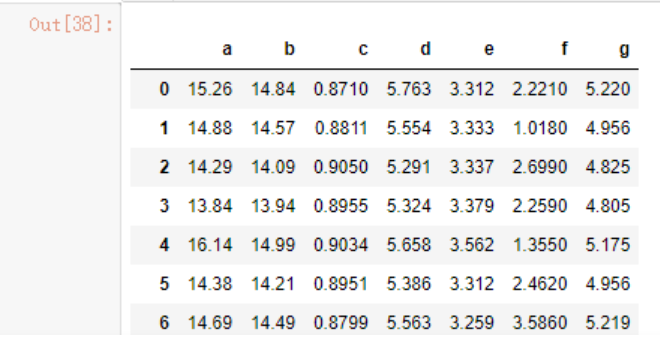
y_predict=KMeans(n_clusters=3).fit_predict(data_x)
y_predict

这里面返回的数字数组并没有什么特殊规定，只是代表某一类的代号，也许你看到的数组以2开头，都是正常的。让我们再开看下原始数据中的Y分类

data.Y

对原始数据的Y分类和我们提取到的y_predict中的比较观察，我们可以发现，预测值（y_predict）中的0应该代表原始数据中的1,1=>2，2=>3，为了方便下面的运算，我们可以先将预测结果的数组array转为一个Series，关于Series的基础知识请查看Pandas初了解-Series

y_predict_se = pd.Series(y_predict)
y_predict_se

再使用Series的map函数将对应的数字映射成一样的，方便下面的运算

info_dict = {0:1,1:2,2:3}
y_pre = y_predict_se.map(info_dict)
y_pre

此时，我们手上有两个Series，y_pre（预测分类）和data.Y（实际分类），我们将其合并在一个DataFrame中通过比较值是否相同就可以知道预测的分类准确率了。

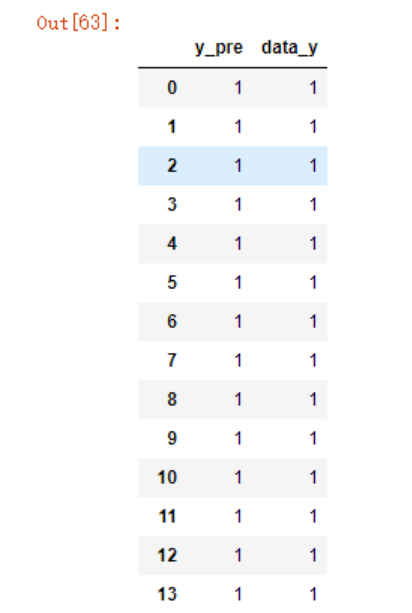
new_df = pd.DataFrame({'y_pre':y_pre,
                      'data_y':data.Y})
new_df

new_df['right'] = new_df.y_pre == new_df.data_y
new_df

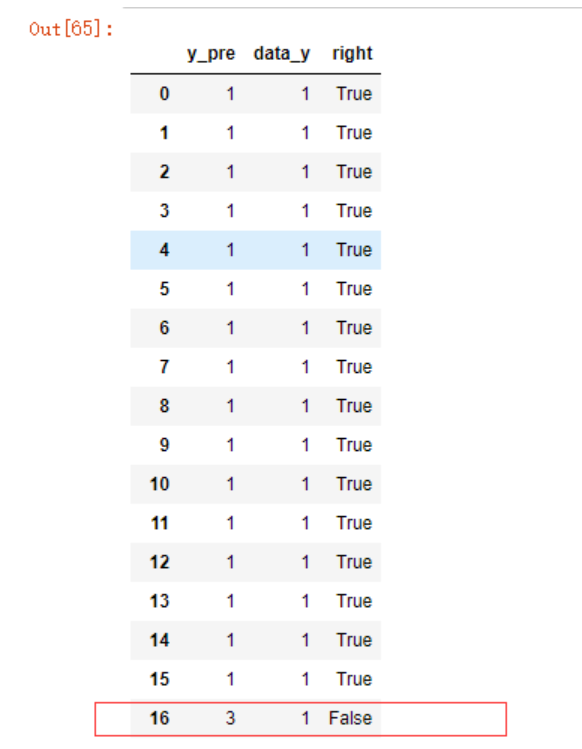
再利用布尔值对应的数值相加，获得最终分类正确数量

new_df.right.sum()
>188
new_df.right.sum()/len(new_df)
>0.8952380952380953

准确率为89%，看起来也还可以。

上面的例子中，我们是已经知道需要分为3类，假设我们不知道分为几类呢？这时候就可以考虑使用calinski_harabasz_score函数来评估模型的靠谱程度了，我们先来算下上面的得分

calinski_harabasz_score(X=data_x,
                       labels=y_predict)

我们现在分为4类看看

y_predict_2=KMeans(n_clusters=4).fit_predict(data_x)
y_predict_2

calinski_harabasz_score(X=data_x,
                       labels=y_predict_2)

数值比3类低，效果不好。

需要注意的是，由于K-Means聚类是以样本间距离为基础，将所有的观测划分到K个群体，使得群体和群体之间的距离尽量大，同时群体内部的观测之间的“距离和”最小，那么使得其对圆形分布的数据分类效果不是很好

上图中的数据点，如果让我们人为来分类，很明显会被分为两类，即内圈一类和外圈一类，但实际上如果使用KMeans算法来进行分类，可能会被分成如下左右两类

YOLO813

机器学习（3）- 聚类KMeans算法初了解