以下数据源来自于互联网公开的北京二手房成交数据，仅作个人学习使用。

数据预处理

    合并数据如下

data.head()

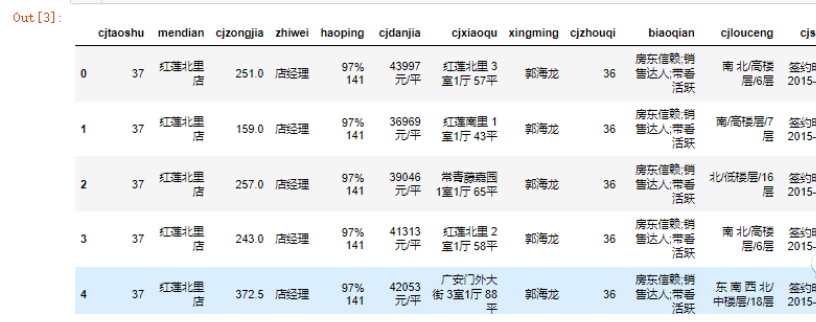
data = data.dropna(how='all')
data.info()

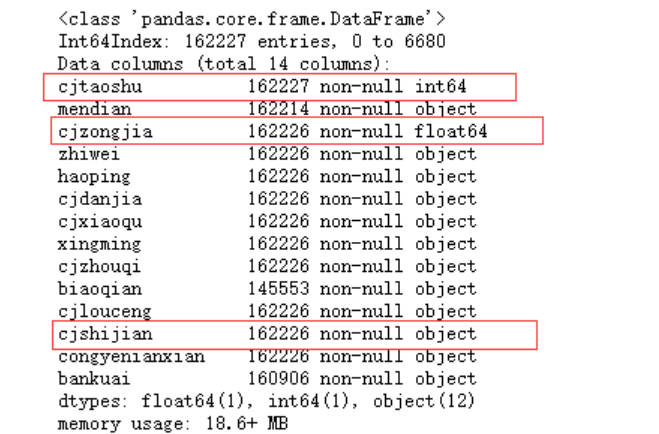
    考虑分析时间和成交单价的关联性，并对某个小区的单价进行预测

    先清洗成交单价字段

data.cjdanjia = np.round((data.cjdanjia.str.replace("元/平","").\
                          astype('float'))/10000,2)
data.cjdanjia

    将其整理成时间序列

data.cjshijian.str.replace("签约时间：","")

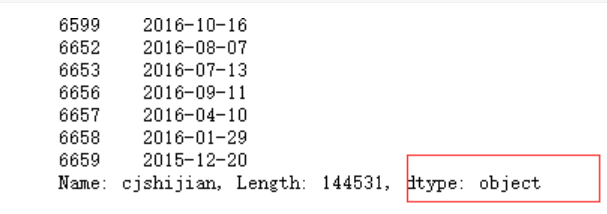
pd.to_datetime(data.cjshijian.str.replace("签约时间：",""))
data.cjshijian = pd.to_datetime(data.cjshijian.str.replace("签约时间：",""))

data.set_index("cjshijian",inplace=True)

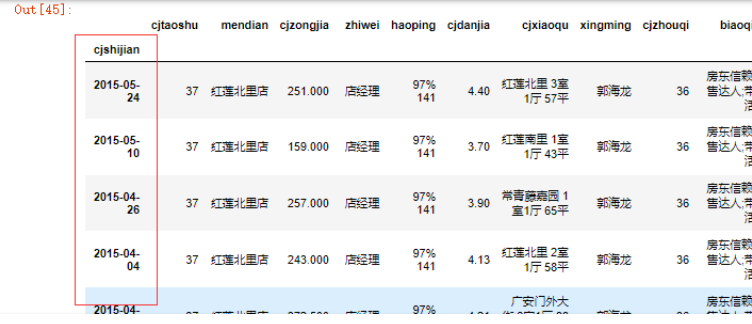
data.index

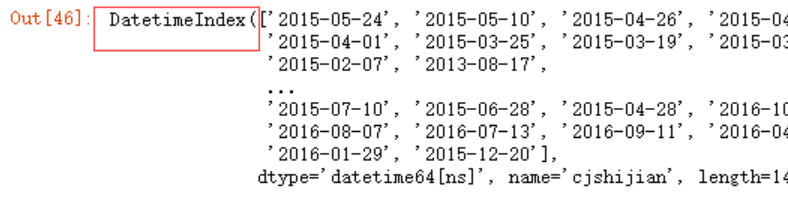
    取得某个小区的数据，并将其排序

data[data.cjxiaoqu.str.contains('远洋山水')]
data = data[data.cjxiaoqu.str.contains('远洋山水')]

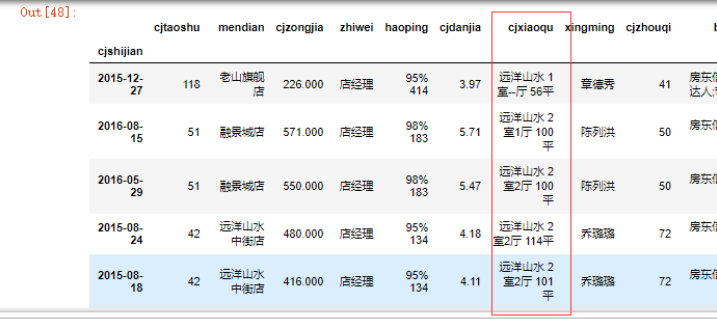
data.sort_values(by='cjshijian')
data = data.sort_values(by='cjshijian')

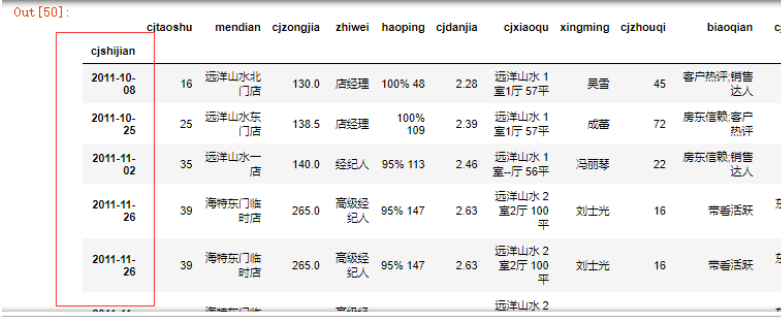
    取出2012年以后的数据（对于时间序列的取值）

data= data["2012":]
data

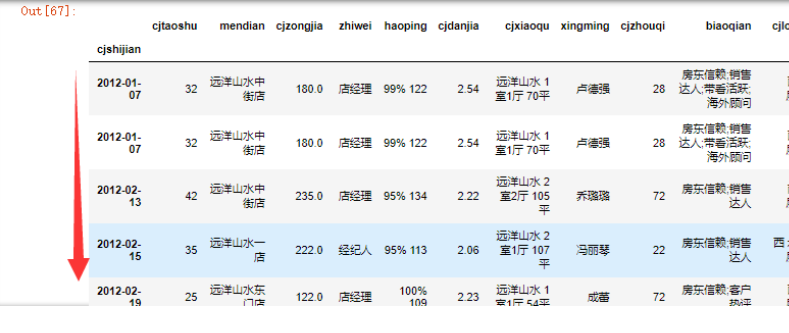
    在建模之前，我们可以先绘图来看下情况，注意，由于cjshijian已经是时间索引了，所以如果使用data.cjshijian是取不到时间值的，我们必须使用index.values来获取其时间数组

plt.figure(figsize=(12,8))
plt.scatter(data.index.values, data.cjdanjia)

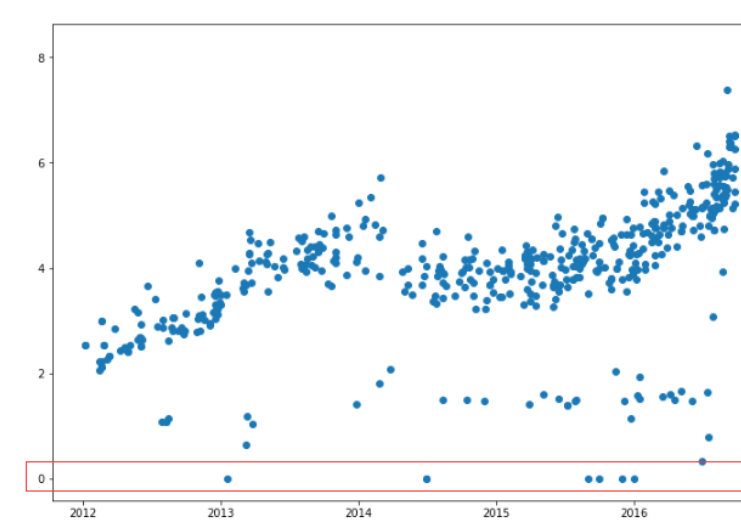
    存在单价为0的数据，我们也一并去掉

data = data[data.cjdanjia>1]
plt.figure(figsize=(12,8))
plt.scatter(data.index.values, data.cjdanjia)

 

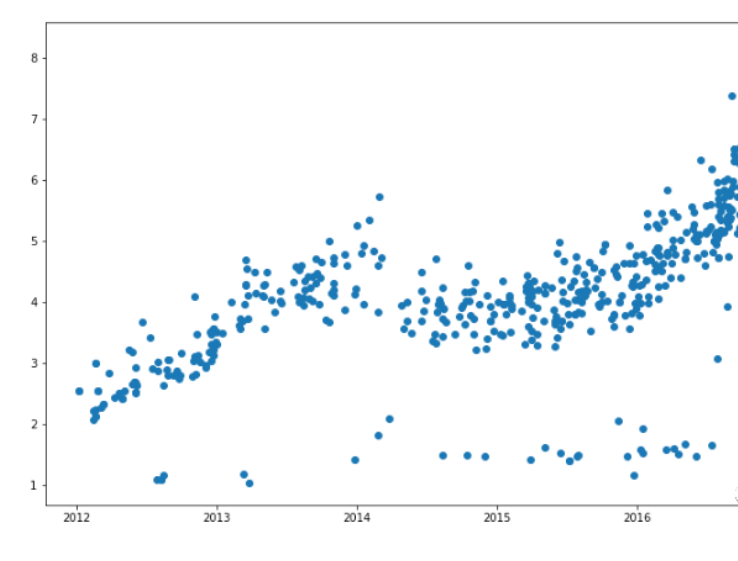
建模测试

    先假设我们不考虑分离训练数据和测试数据，将全部数据用于建模。

    我们可以考虑将日期转换为天数，更方便运算。例如，以2012年1月1日为起点开始计算

data.index - pd.to_datetime("2012-01-01")

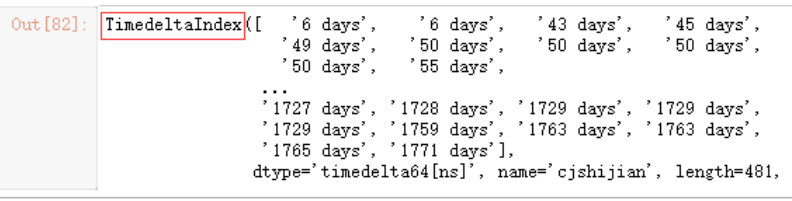
(data.index - pd.to_datetime("2012-01-01")).days

    此时如果直接赋值，如下面这种方法，可能会有警告

data['time'] = (data.index.copy() - pd.to_datetime("2012-01-01")).days

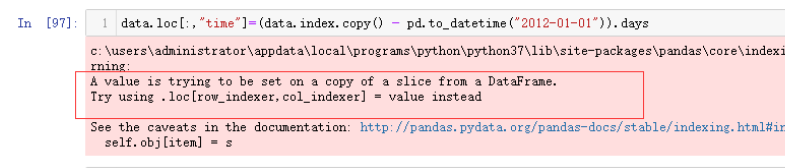
    建议使用assign方法

data = data.assign(time = (data.index - pd.to_datetime("2012-01-01")).days)

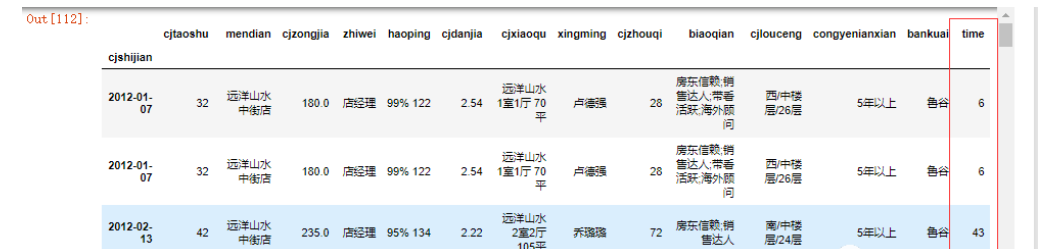
    取出需要的值

data = data[['cjdanjia','time']]
data

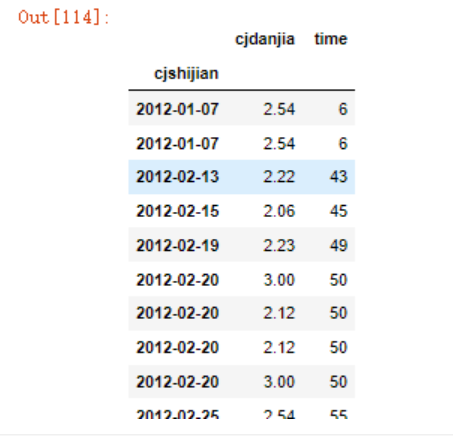
plt.figure(figsize=(12,8))
plt.scatter(data.time, data.cjdanjia)

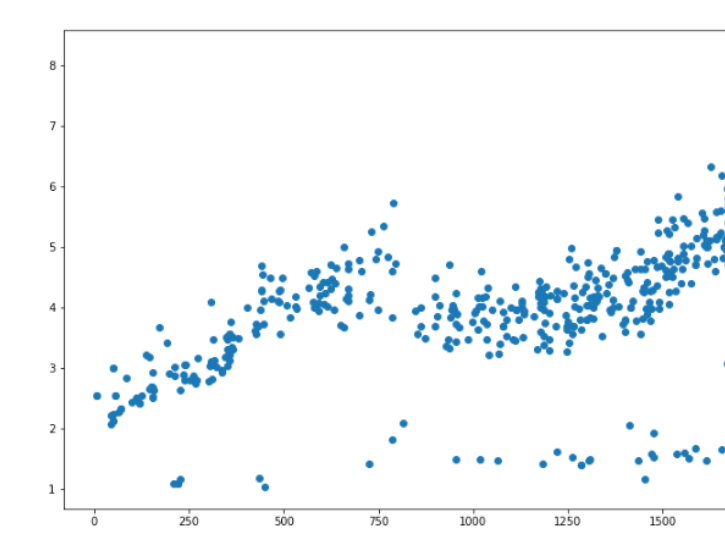
    先尝试一元建模

from sklearn.linear_model import LinearRegression
model1 = LinearRegression()
model1.fit(data.time, data.cjdanjia)

    这时会报错，因为data.time的形状不符合要求，我们来看下data.time，它是一个Series，并没有reshape方法，我们可以将其转为数组类型

data.time

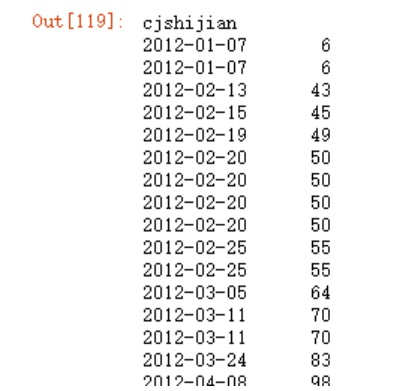
data.time.values

model1.fit(data.time.values.reshape(-1,1), data.cjdanjia)
# 也可以直接将data.time转为DataFrame
model1.fit(pd.DataFrame(data.time), data.cjdanjia)

    绘图查看情况

#制作x轴数据来看下曲线情况
x1 = np.linspace(0,1900,num=100)
y1 = model1.predict(x1.reshape(-1,1))
plt.figure(figsize=(12,8))
plt.scatter(data.time, data.cjdanjia)
plt.plot(x1,y1,'r')

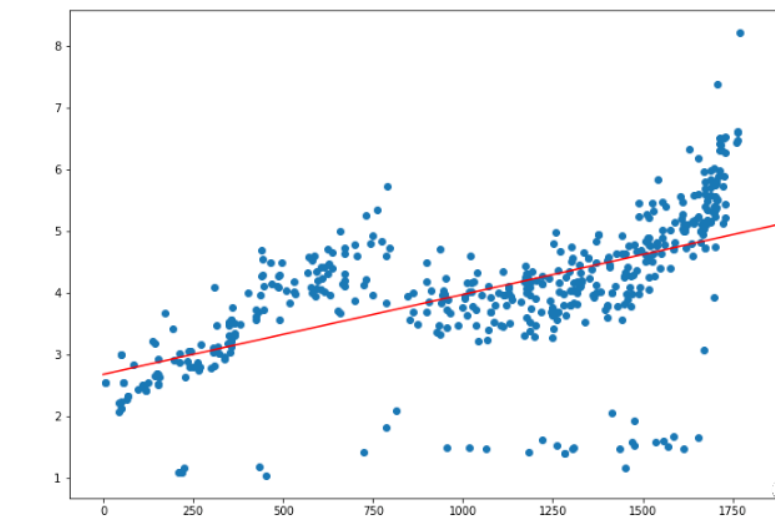
    可以看到，效果很差。

 

多项式回归

    形如f(x)=an·x^n+an-1·x^(n-1)+…+a2·x^2+a1·x+a0的函数，叫做多项式函数，它是由常数与自变量x经过有限次乘法与加法运算得到的。显然，当n=1时，其为一次函数y=kx+b，当n=2时，其为二次函数。

    一般地，形如y=ax^2+bx+c的函数叫做二次函数（quadratic function）。其图像在平面直角坐标系中呈一条抛物线。

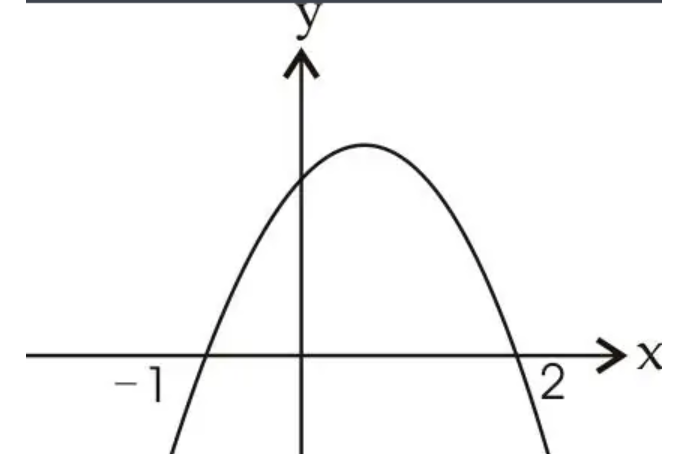
    形如 y=ax^3+bx^2+cx+d (a≠0,b,c,d为常数)的函数叫做三次函数(cubics function)。三次函数的图像是一条曲线——回归式抛物线（不同于普通抛物线），具有比较特殊的性质。

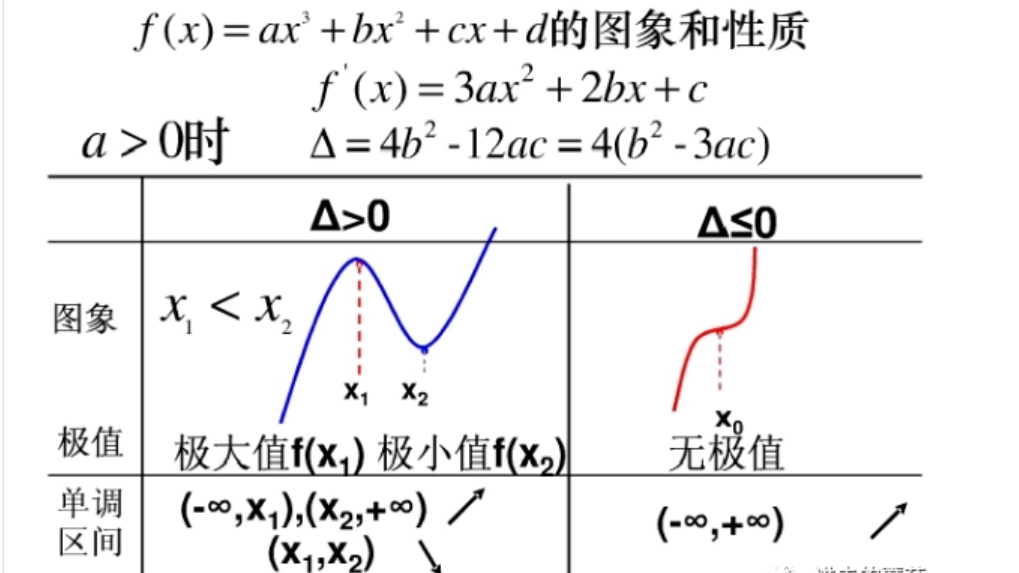
    由于绘制的散点图形状，所以考虑多项式回归模型。

    根据公式y=ax^2+bx+c，所以这次的X轴需要将x^2和x一同输入进去

#将所有数据按照公式丢入进来
X = pd.DataFrame({"x1":data.time**2,
           'x2':data.time})
Y = data.cjdanjia
X[:5]

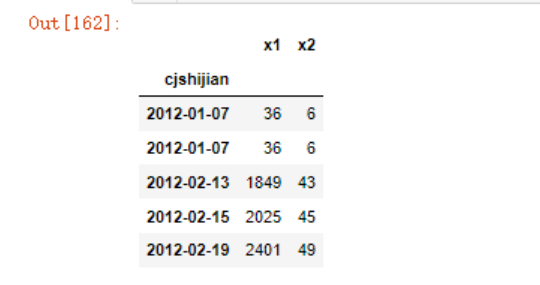
model2 = LinearRegression()
model2.fit(X,Y)

#为什么自制x轴坐标？
#可以想象以下，如果使用原始数据的X
#他有两个点，根本无法确定
x2 = np.linspace(0,1900,num=100)
#这里面预测的点就使用上面的x2坐标
y2 = model2.predict(pd.DataFrame({"x1":x2**2,
           'x2':x2}))
plt.figure(figsize=(12,8))
plt.scatter(data.time, data.cjdanjia)
plt.plot(x2,y2,'r')

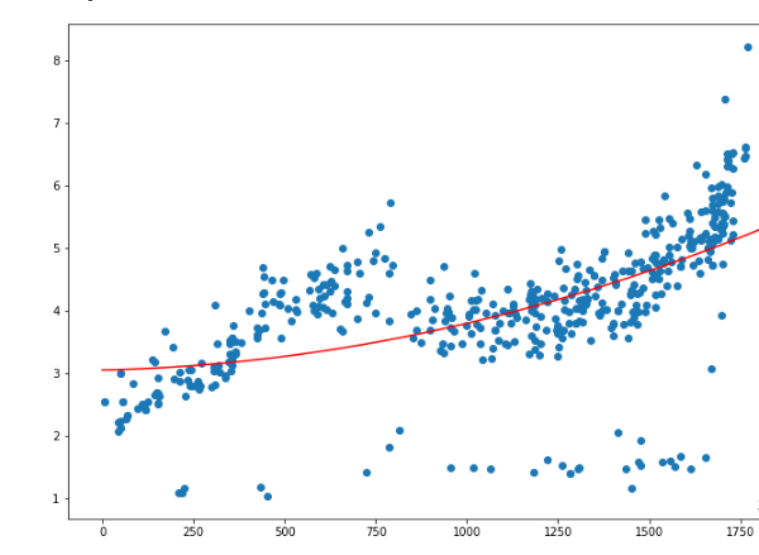
    二次回归的效果稍微强点，但也不是特别符合，可以考虑使用三次函数来建模。

    我们可以继续使用前面的方法来构造方程式，但是挺麻烦的，sklearn中有一个preprocessing.PolynomialFeatures可以快速帮我们构造多项式，

from sklearn.preprocessing import PolynomialFeatures

#初始化几次函数
q3 = PolynomialFeatures(degree=3)

X3 = q3.fit_transform(pd.DataFrame(data.time))
X3

model3= LinearRegression()
model3.fit(X3, Y)

x3 = np.linspace(0,1900,num=100)
#我们需要把待预测的x3也变成多项式
x_ = q3.fit_transform(pd.DataFrame(x3))
# y2 = model3.predict(pd.DataFrame({"x1":x3**2,
#            'x2':x2}))
y3 = model3.predict(x_)
plt.figure(figsize=(12,8))
plt.scatter(data.time, data.cjdanjia)
plt.plot(x3,y3,'r')

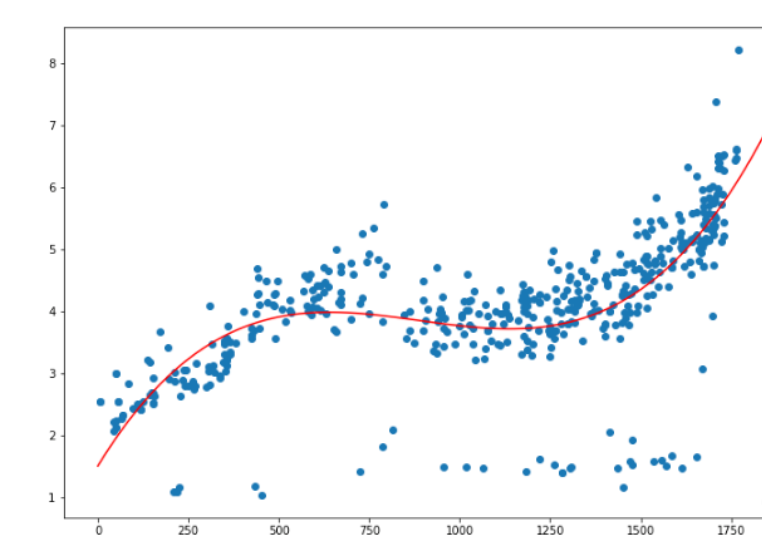
    同理，我们可以快速的使用4次函数建模

q4 = PolynomialFeatures(degree=4)
X4 = q4.fit_transform(pd.DataFrame(data.time))
model4= LinearRegression()
model4.fit(X4, Y)

x4 = np.linspace(0,1900,num=100)
#我们需要把x3也变成多项式
x_ = q4.fit_transform(pd.DataFrame(x4))
y4 = model4.predict(x_)
plt.figure(figsize=(12,8))
plt.scatter(data.time, data.cjdanjia)
plt.plot(x3,y3,'g')
plt.plot(x4,y4,'r')

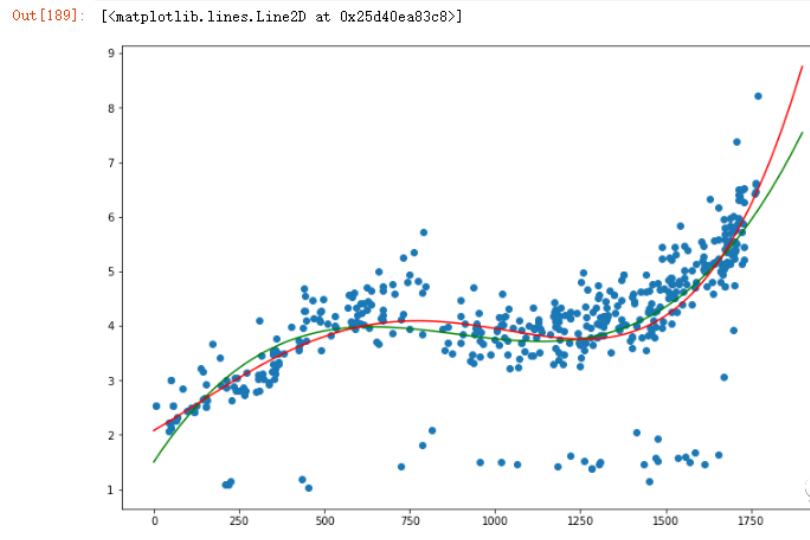
    到这里，你会发现似乎没有一个好的办法去评估自己的模型，因为所有数据都用于建模训练了，所以，对于线性回归，最好还是分成训练数据和测试数据。

    需要注意的是，因为这些数据具有先后时间关系，就无法使用之前那种乱序划分 train_test_split方法了。

x_train,x_test = data[:"2016-05"].time,data["2016-05":].time
x_train[:5]

y_train,y_test = data[:"2016-05"].cjdanjia,data["2016-05":].cjdanjia
y_train[:5]

q3 = PolynomialFeatures(degree=3)
x3 = q3.fit_transform(pd.DataFrame(x_train))
model3 = LinearRegression()
model3.fit(x3, y_train)

#使用模型预测
x_ = q3.fit_transform(pd.DataFrame(x_test))
y_pre = model3.predict(x_)
y_pre

#导入函数计算差均值
from sklearn.metrics import mean_squared_error

mean_squared_error(y_test,y_pre)

#四项函数
q4 = PolynomialFeatures(degree=4)
x4 = q4.fit_transform(pd.DataFrame(x_train))
model4 = LinearRegression()
model4.fit(x4, y_train)

x_ = q4.fit_transform(pd.DataFrame(x_test))
y_pre = model4.predict(x_)
y_pre

mean_squared_error(y_test,y_pre)

    可以看到，四次函数的拟合度更好。