机器学习（11）- 支持向量机初了解

支持向量机（Support Vector Machine），是一类按监督学习（supervised learning）方式对数据进行二元分类的广义线性分类器（generalized linear classifier），其决策边界是对学习样本求解的最大边距超平面（maximum-margin hyperplane）。

推荐两篇SVM的介绍文章，链接放在参考中。

SVM可以做什么？

处理分类任务或回归任务。但是，它主要适用于分类问题。

适用范围？

适合应用于复杂但中小规模数据集的分类问题。

算法原理？

求解能够正确划分训练数据集并且几何间隔最大的分离超平面。支持向量机进行分类，是为了得到一个分类器或分类模型，这个分类器是一个超平面（如果数据集是二维，这个超平面就是直线，三维数据集，就是平面，以此类推），这个超平面把样本一分为二，当然，这种划分不是简单划分，需要使正例和反例之间的间隔最大。间隔最大，其泛化能力就最强。

硬间隔和软间隔？

硬间隔只对线性可分的数据起作用，我们可以使用SVM的C超参数（惩罚系数或者松弛系数）来控制超平面的位置，在数据违规和支持向量的距离之间找一个平衡点，较小的C会导致支持向量到超平面的距离更大，但也可能导致更多的间隔违规（样本的错误划分）。

过拟合的解决办法？

可以通过减小C的系数，让支持向量到超平面的距离更大来缓解。

核函数有几种？

线性核函数：简单效率高；对线性不可分的误解。
多项式核函数：可拟合出复杂的分割超平面，但可选参数太多，阶数高后计算困难，不稳定。
高斯核函数:融合了上面两种核函数。计算速度比较慢，容易过拟合。

为什么要用核函数？

例如下方的第二张图片，即使使用了松弛变量，也很难达到满意的效果，这时候就可以通过核函数把线性不可分数据集转换为线性可分（在更高维度空间中）。

分类问题如何选择算法？逻辑回归还是SVM？如果使用核函数选择哪一种比较好？

假如，N种特征，M个训练集样本：

如果N>M，使用逻辑回归或线性核函数的SVM算法都可以。
N较小，M是N的10倍左右，可使用高斯核函数。
N较小，M是N的50倍以上，可使用多项式核函数或高斯核函数。

sklearn中实现的SVM算法？

Kernel指定核函数：

Linear线性函数：C惩罚系数
Poly多项式：C惩罚系数，degree指定阶数
Rbf 高斯核函数：C惩罚系数，gamm值

举个例子，现在我想要将下面的两个图形分开，并使得样本（任一类）到该条线的距离最远，选择哪条线更合适？

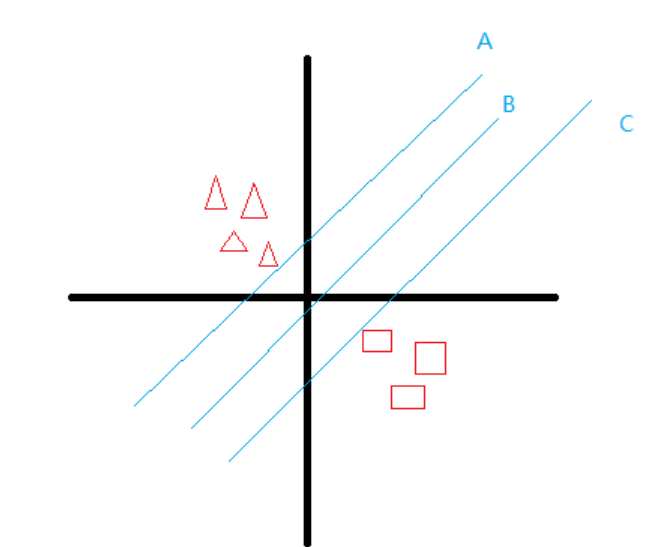
很明显，选择B线，因为样本最近的数据点（任一类）和超平面之间的距离最大化了，其中最近的数据点定义为支持向量。

但假如样本的分布是这种呢？

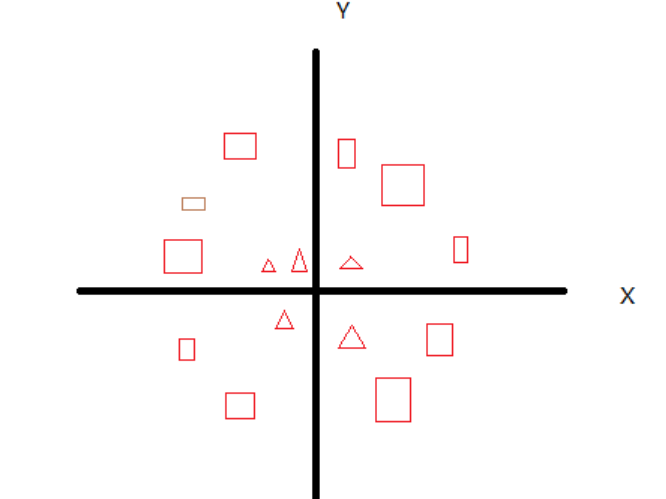
这时候就体现出SVM核函数的威力了，将二维平面的点映射到三维来进行划分，例如

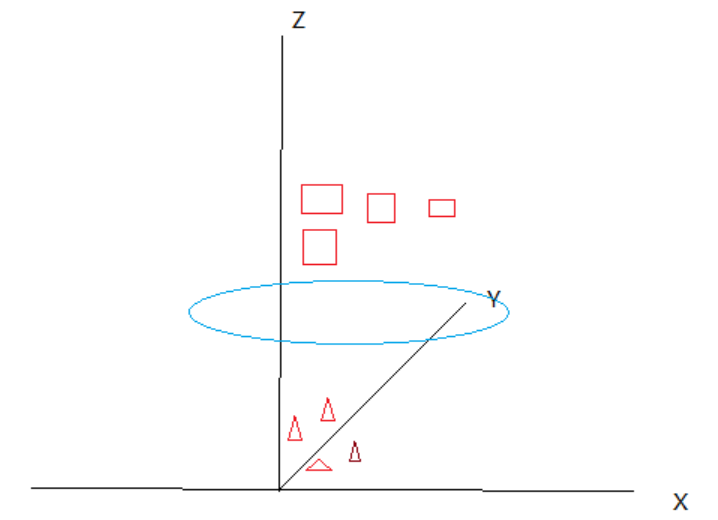
所有样本点的XY坐标不变，只是增加了一个样本点到到原点的距离（x的平方+y的平方的算术平方根），这样就可以利用一个超平面将两个数据完美划分。我想，这应该也是使用SVM时需要对数据进行标准化处理的原因之一吧。

照例，来个官方参数文档：

Init signature:
SVC(
    *,
    C=1.0,
    kernel='rbf',
    degree=3,
    gamma='scale',
    coef0=0.0,
    shrinking=True,
    probability=False,
    tol=0.001,
    cache_size=200,
    class_weight=None,
    verbose=False,
    max_iter=-1,
    decision_function_shape='ovr',
    break_ties=False,
    random_state=None,
)

数据实例，德国信用卡欺诈（之前使用逻辑回归算法）：

data.head()

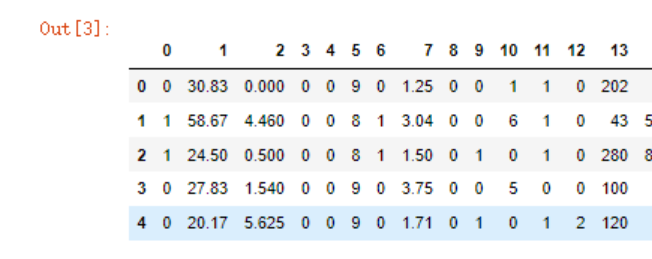
data_train = data[data.columns[:-1]]
data_test = data[data.columns[-1:]].replace(-1,0)
x_train,x_test,y_train,y_test = train_test_split(data_train,data_test)

#数据标准化
from sklearn import preprocessing
scaler = preprocessing.StandardScaler().fit(x_train)
#注意下面的缩放特征要与其保持一致
#使用同一个scaler
x_train = scaler.transform(x_train)
x_test = scaler.transform(x_test)

导入SVC

from sklearn.svm import SVC

#线性核函数
model = SVC(kernel='linear')
model.fit(x_train,y_train.values.flatten())
model.score(x_test,y_test)
>0.8597560975609756

#多项式
model2 = SVC(kernel='poly',
            degree=3,
            C=5)
model2.fit(x_train,y_train.values.flatten())
model2.score(x_test,y_test)
>0.8597560975609756

#高斯核函数
model3 = SVC(kernel='rbf',
            degree=3,
            gamma=0.5)
model3.fit(x_train,y_train.values.flatten())
model3.score(x_test,y_test)
>0.7865853658536586

参考：

http://www.feiguyunai.com/index.php/2017/10/25/pythonai-svm01/
https://zhuanlan.zhihu.com/p/71074401
# 数据标准化
https://blog.csdn.net/sunlilan/article/details/71512223

YOLO813

机器学习（11）- 支持向量机初了解