机器学习（2）- 多元线性回归模型的了解

关于多元线性回归，指的是在回归分析中，如果有两个或两个以上的自变量，例如方程式

y=a*x1+b*x2+c*x3+d

存在三个自变量x1，x2，x3，截距（intercept_）d，三个斜率（coef_）a、b、c。

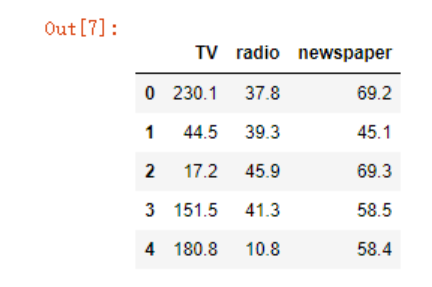
以下分析的数据Advertising.csv，数据集包含了200个不同市场的产品销售额，每个销售额对应3种广告媒体投入成本，分别是：TV, radio, 和 newspaper，现在我们要根据三种媒体的广告投入，来预测销售额

data = pd.read_csv('./Advertising.csv')
df = data[["TV","radio","newspaper","sales"]]
df

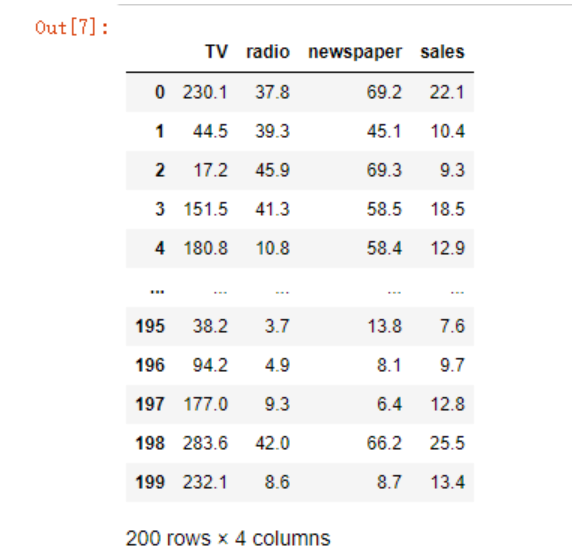
我们推测，以上三项都对销售额具有影响，而且是一种线性正相关，考虑使用多元回归模型来解决问题，并使用均方误差（Mean squared error）作为评价标准。

#导入线性回归模型类
from sklearn.linear_model import LinearRegression
#快速将原始数据按照比例分割为“测试集”和“训练集”
from sklearn.model_selection import train_test_split
#导入均方误差
from sklearn.metrics import mean_squared_error

线性回归类上一篇文章中已经介绍过，我们来看下train_test_split，将数组或矩阵拆分为随机训练和测试子集，照例先甩出官方文档

Signature:
train_test_split(    
    *arrays,    
    test_size=None,    
    train_size=None,    
    random_state=None,    
    shuffle=True,    
    stratify=None,
)
Split arrays or matrices into random train and test subsets

test_size如果不设置，则取决于train_size的大小，如果train_size也不设置，则test_size默认为25%。

上面我们只是推测三种广告媒体和销售额有线性惯性，但是并不确定，我们可以以某一媒体为X轴，销售额为Y轴，绘图来观察下

plt.figure(figsize=(8,6))
plt.scatter(df.TV, df.sales)

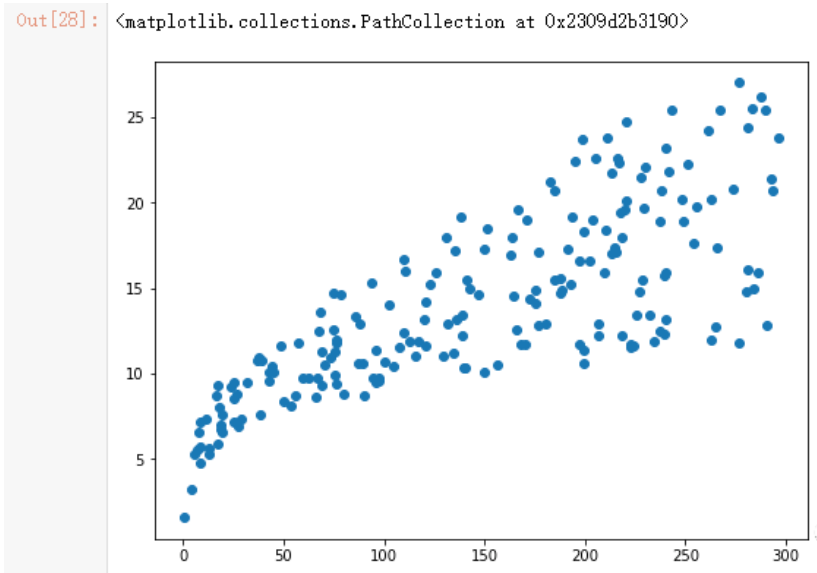
plt.scatter(df.radio, df.sales)

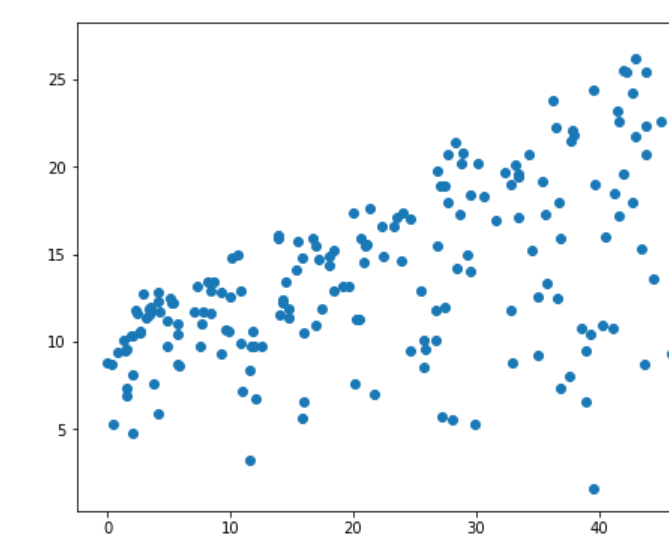
plt.scatter(df.newspaper, df.sales)

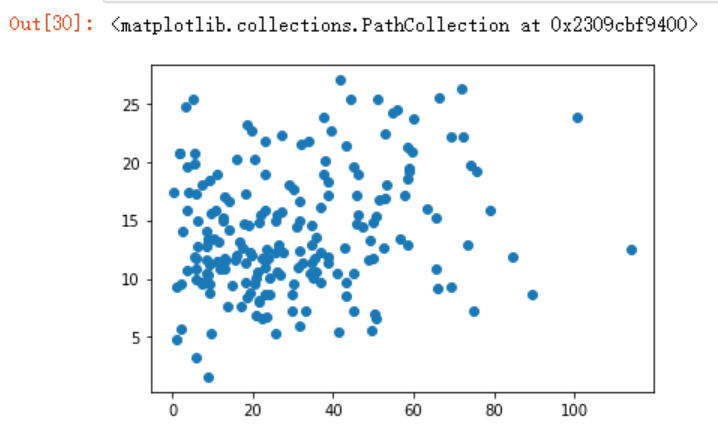
从上面三种图形来看，只有报纸跟销售额的线性关系不大。

当然，这是我们肉眼观察的结果，对于准确的预测没有任何意义，我们现在需要建立模型，然后对模型中的变量和模型进行评估。

获取数据

x = data[["TV","radio","newspaper"]]
x.head()

y = data['sales']
y.head()

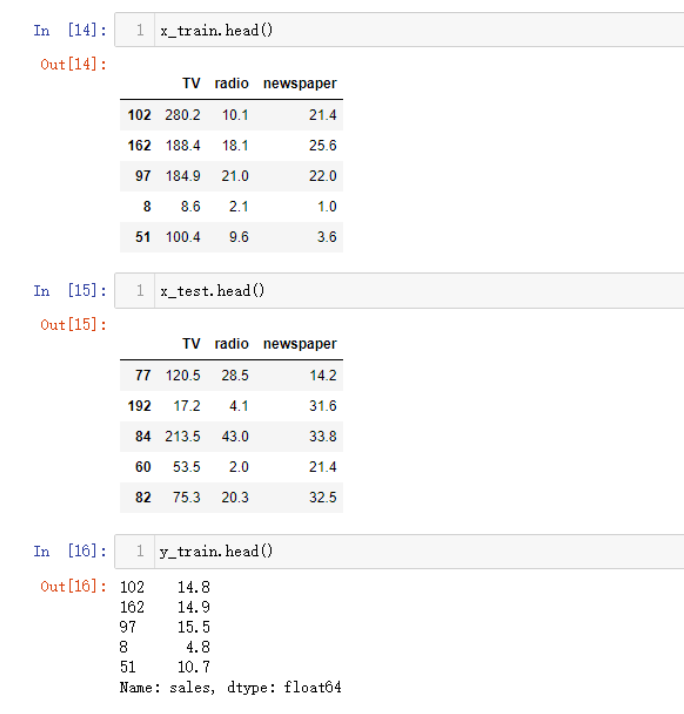
利用train_test_split快速的生成乱序的训练集和测试集。

x_train,x_test,y_train,y_test = \
train_test_split(x, y)

#数据准备好之后，初始化模型
model = LinearRegression()

model.fit(x_train, y_train)

我们可以使用coef来查看下模型的系数（斜率），如下，可以看到返回了一个数组列表，里面存在三个值，还记得上面我写过的多元线性回归方程式吗？y=a*x1+b*x2+c*x3+d，其中斜率abc对应着下面数组中的三个值，而d则对应着截距值

model.coef_
>array([0.04304552, 0.19421789, 0.00687972])
model.intercept_
>3.138584515720872

我们可以将列名取出来看的更为清楚一点

for i in zip(x_train.columns, model.coef_):
    print(i)

我们知道，斜率越大，则直线与x正半轴的角度越大，测试如下

x = np.arange(-10,10)
y0 = 3*x
y = 2*x
y1=0.4*x
plt.plot(x,y0,'--g',x,y,'--b',x,y1,'--y')
plt.axhline(0,c='r')
plt.axvline(0,c='r')

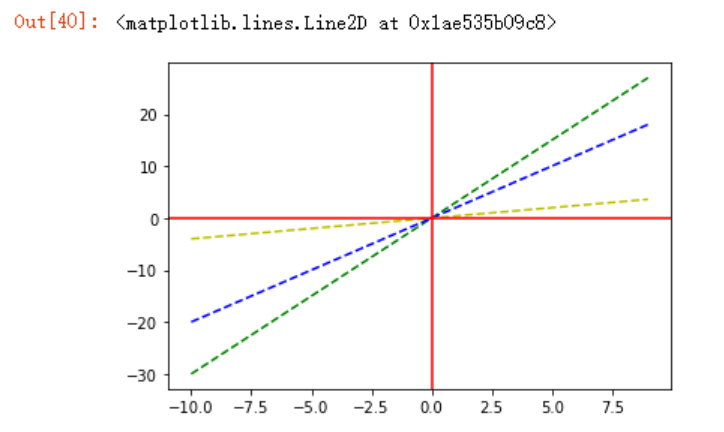
对于多元线性回归方程式来说，道理也是一样的，我们再看一眼这个系数

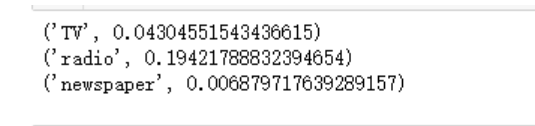
即在TV和newspaper这两个变量不变时，radio每投入100，其销售额增加100*0.1942....。所以，从模型中得到的反馈为radio对sales的正影响最大，而newspaper最小。

对模型的评价，上一篇文章中的一元线性是采用预测值和实际值之间的平方差，多元线性回归也是同样的道理，只不过使用sklearn封装好的mean_squared_error方法。官方文档参数如下

Signature:
mean_squared_error(
    y_true,
    y_pred,
    *,
    sample_weight=None,
    multioutput='uniform_average',
    squared=True,
)

mean_squared_error(y_test, model.predict(x_test))
>4.663462133130601

在mean_squared_error函数中，将预测值y_pred或者测试值y_true调换顺序对结果没有影响，因为最终都是要取值差平方，上面的计算得到了一个数值4.66，我们只知道这个数值越小越好，单独看这个数值没有任何意义，我们可以新建一个模型，再次获取mean_squared_error值进行比较。

由于上面的模型参数中，newspaper参数对sales的影响最小，所以考虑去除这个参数，重新测试。

x1 = data[["TV","radio"]]
y1 = data['sales']
x_train,x_test,y_train,y_test=train_test_split(x1, y1)

model = LinearRegression()
model.fit(x_train, y_train)
mean_squared_error(y_test, model.predict(x_test))
>2.780833947375159

可以明显看到这个模型的效果更好。

总结，线性回归，是一种假设性很强的模型，当我们取得的参数（特征）没有与因变量之间有太多的联系时，过多的自变量反而会导致模型的准确率降低。

YOLO813

机器学习（2）- 多元线性回归模型的了解