机器学习（7）- KMeans的不足以及DBSCAN算法的应用

以下数据源来自于互联网公开的北京二手房成交数据，仅作个人学习使用。

在网上找到一张关于K-means算法的图片，很形象。

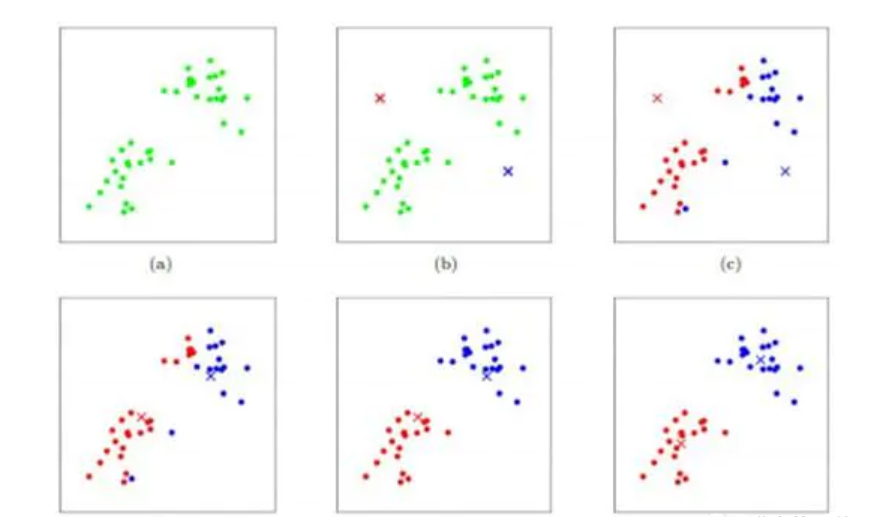
数据样本用圆点表示，每个簇的中心点用叉叉表示。(a)刚开始时是原始数据，杂乱无章，没有label，看起来都一样，都是绿色的。(b)假设数据集可以分为两类，令K=2，随机在坐标上选两个点，作为两个类的中心点。(c-f)演示了聚类的两种迭代。先划分，把每个数据样本划分到最近的中心点那一簇；划分完后，更新每个簇的中心，即把该簇的所有数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”，直到每个簇的中心不在移动为止。

关于K-Means的不足，之前简单了解了下，但不系统，以下内容摘录之互联网：

在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。
在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果，这也成为 K-means算法的一个主要问题。
K-means算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。

先来看下使用KMeans算法的聚类

data1 = data[data.cjxiaoqu.str.contains('龙锦苑东一区 3室2厅 124平')]

plt.scatter(np.arange(1, len(data1)+1), data1.cjdanjia)

from sklearn.cluster import KMeans
y_pre = KMeans(n_clusters=2).fit_predict(data1.cjdanjia.values.reshape(-1,1))
plt.scatter(np.arange(1, len(data1)+1),
            data1.cjdanjia,
           c =y_pre)

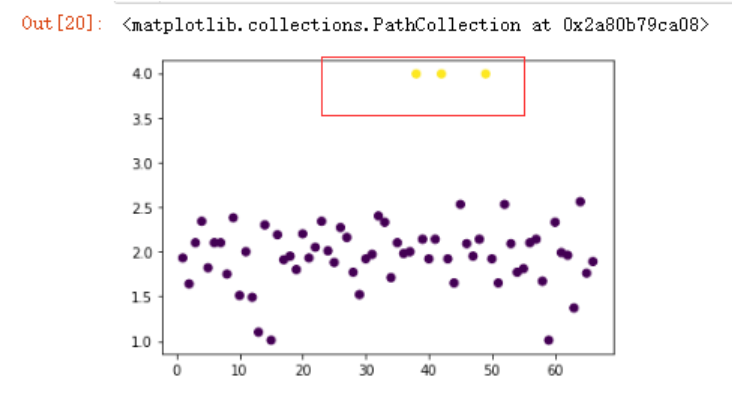
成功将几个价格较高的数据聚成一类，再看下一个例子

data2 = data[data.cjxiaoqu.str.contains('龙锦苑东五区 3室2厅 124平')]

plt.scatter(np.arange(0, len(data2)), data2.cjdanjia)

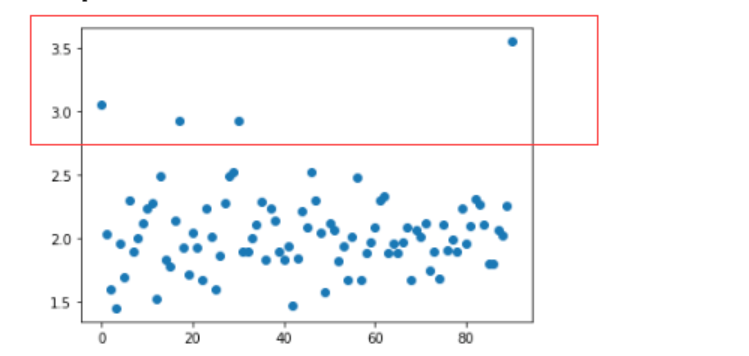
现在假设我想要将上面四个较高的价格分为一类

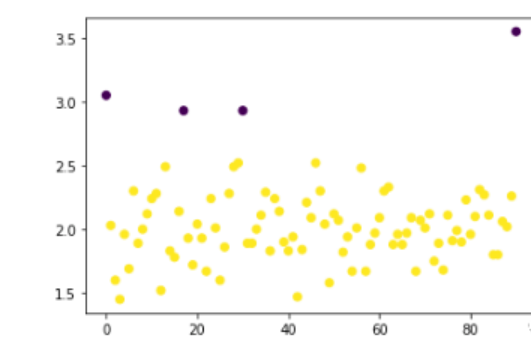
y_pre2 = KMeans(n_clusters=2).fit_predict(pd.DataFrame(data2.cjdanjia))
plt.scatter(np.arange(0, len(data2)),
            data2.cjdanjia,
           c =y_pre2)

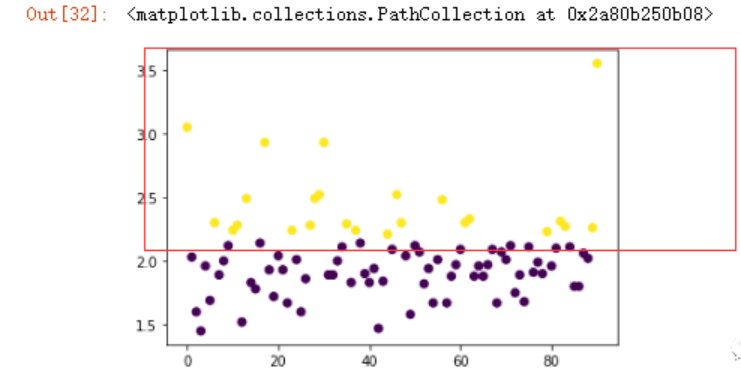
可以看到聚类的结果不符合我们的要求。

DBSCAN算法

和KMeans算法基于距离不一样，DBSCAN是基于密度来进行聚类。

聚类的时候不需要预先指定簇的个数
最终的簇的个数不确定

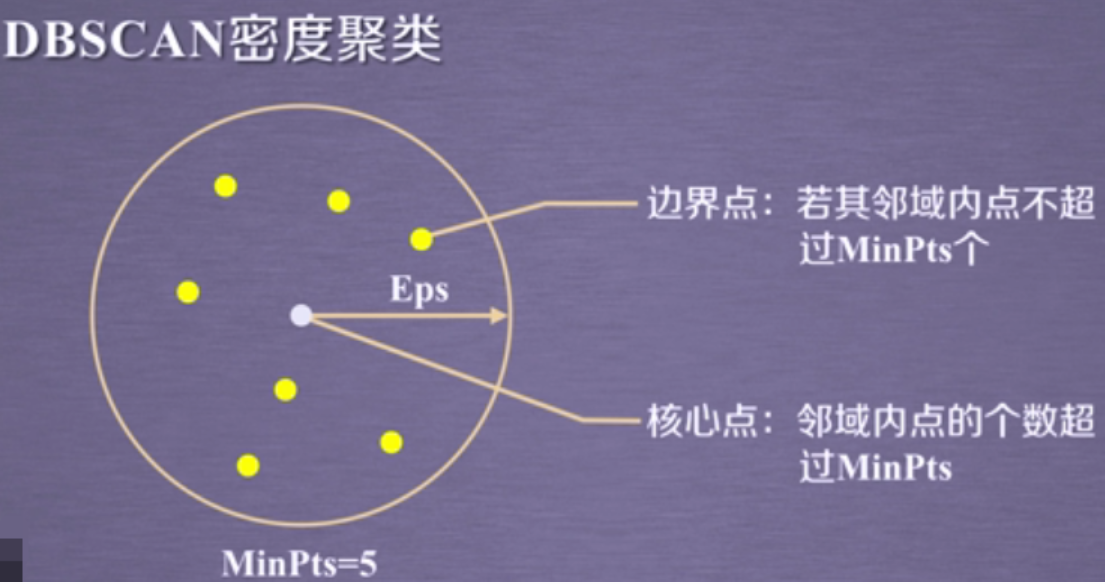
DBSCAN算法将数据点分为三类：

核心点：在半径Eps内含有超过MinPts数目的点。
边界点：在半径Eps内点的数量小于MinPts,但是落在核心点的邻域内的点。
噪音点：既不是核心点也不是边界点的点。

官方介绍：

Init signature:
DBSCAN(
    eps=0.5,
    *,
    min_samples=5,
    metric='euclidean',
    metric_params=None,
    algorithm='auto',
    leaf_size=30,
    p=None,
    n_jobs=None,
)

示例

from sklearn.cluster import DBSCAN
ypre3 =DBSCAN(eps=0.5).fit_predict(data2[['cjdanjia']])
plt.scatter(np.arange(0, len(data2)),
            data2.cjdanjia,
           c =ypre3)

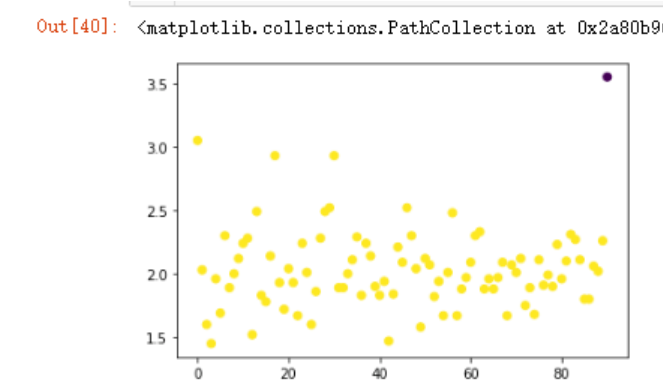
默认的参数看起来没什么区别，调整一下密度

ypre4 =DBSCAN(eps=0.3).fit_predict(data2[['cjdanjia']])
plt.scatter(np.arange(0, len(data2)),
            data2.cjdanjia,
           c =ypre4)

再次调整密度，让其价格区间聚类再密集一点

ypre5 =DBSCAN(eps=0.1).fit_predict(data2[['cjdanjia']])
plt.scatter(np.arange(0, len(data2)),
            data2.cjdanjia,
           c =ypre5)

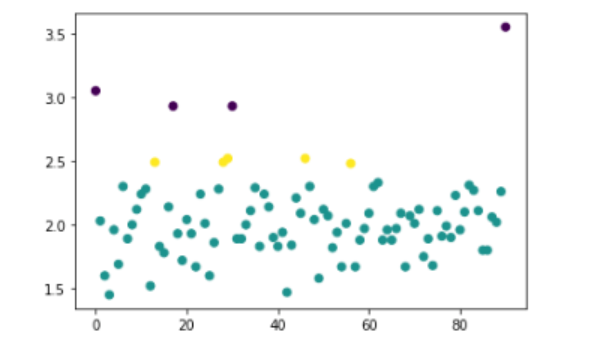
这个用途在于，假如想要监控某一个价格区间的房价数据，一旦有不在这个区域内的价格，那么聚类之后立刻就可以获知。

参考

https://www.jianshu.com/p/9348e5a9f0dd
https://www.cnblogs.com/bonelee/p/8692336.html
https://blog.csdn.net/huacha__/article/details/81094891

YOLO813

机器学习（7）- KMeans的不足以及DBSCAN算法的应用